Actual Mating Envelope
When we want to know how big a hole or a pin or a slot is, or if we want to know the axis or center-plane of a hole or a pin or a slot, we must agree on how to define those sizes and axis or center-planes. Real parts are never straight or perfectly round or perfectly square. So our definition must acknowledge these imperfections.
We use something called an Actual Mating Envelope. First we'll talk about how this applies to holes or pins.
Imagine an envelope that we can roll into a perfect cylinder. The diameter of this perfect cylinder can get bigger or smaller as required.
We use something called an Actual Mating Envelope. First we'll talk about how this applies to holes or pins.
Imagine an envelope that we can roll into a perfect cylinder. The diameter of this perfect cylinder can get bigger or smaller as required.
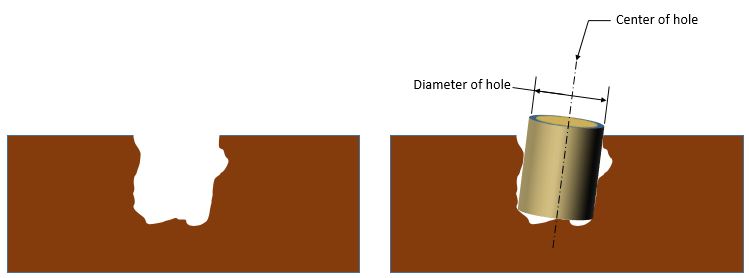
Imagine that a dog digs a hole like the one on the left below. We want to know what the diameter of the hole is and what the axis of the hole is. So we take our envelope and roll it into a perfect cylinder as shown on the right below. We put the envelope in the hole and expand it until it just perfectly touches the sides of the hole. It's a best fit, and it's not necessarily perpendicular to the ground. It's on whatever angle the best fit happens to be. The diameter of this envelope then is defined as the diameter of the hole. Also the axis of this envelope is defined as the axis of the hole.
Likewise if we have a pin, or in this case a long dog toy, and we want to know its diameter and its axis. In this case we will just focus on the body of the dog toy. It's not a nice cylinder. It's kind of rough and a little bit curved. So we take our envelope and roll it into the smallest perfect cylinder that will fit around the body of the toy. The diameter of the cylinder now is defined as the diameter of the body of the toy. And the axis of the cylinder is defined as the axis of the body of the toy.
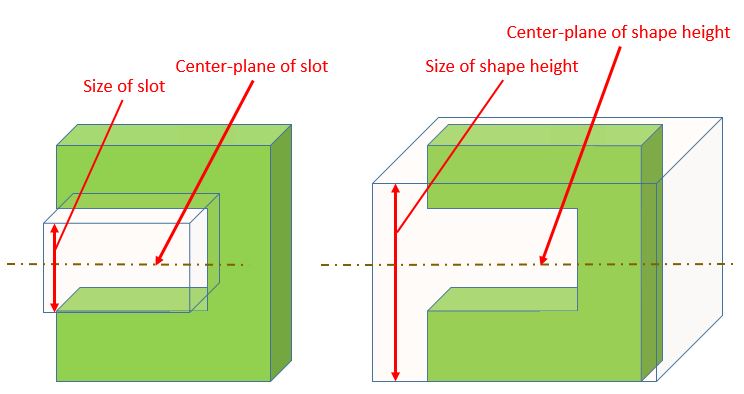
The same applies to rectangular shapes. In the figure below, on the left, we insert the largest perfect box that will fit into the slot. The largest perfect box that will fit is called the Actual Mating Envelope. The height of the box then is defined to be size of the slot. The center-plane of the box is defined to be the center-plane of the slot.
In the figure below on the right, we find the smallest perfect box that will fit over the part. The smallest perfect box that will fit over the part is called the Actual Mating Envelope. The height of this box is defined to be the height of the part. The center-plane of this box is defined to be the center-plane of the part.
In the figure below on the right, we find the smallest perfect box that will fit over the part. The smallest perfect box that will fit over the part is called the Actual Mating Envelope. The height of this box is defined to be the height of the part. The center-plane of this box is defined to be the center-plane of the part.
All of the Actual Mating envelopes shown above are Unrelated Actual Mating Envelopes.
Now we need to talk about related vs. unrelated Actual Mating Envelopes.
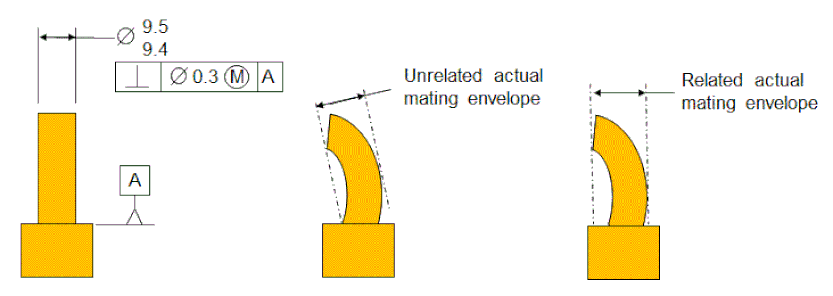
The figure below shows a pin that has a size and a perpendicularity relative to a datum.
The center of the figure shows that the Unrelated Actual Envelope is the smallest perfect cylinder that will fit over the physical cylinder without regard to the datum. Most of the time, the Unrelated Actual Mating Envelope will almost never be perfectly perpendicular to the datum.
The right side of the figure shows that the Related Actual Mating Envelope is the smallest perfect cylinder that is perpendicular to the datum and fits around the physical cylinder. The Related Actual Mating Envelope is always perpendicular to the datum.
The size of the Unrelated Actual Mating Envelope is considered to be the size of the pin.
The axis of the Unrelated Actual Mating Envelope is considered to be the axis of the pin.
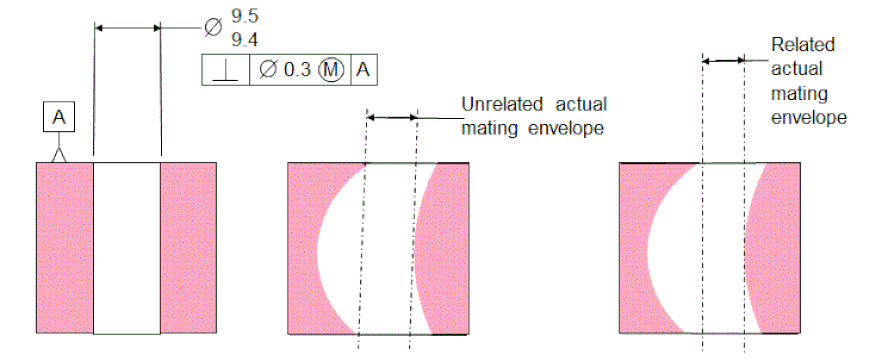
The figure below shows Actual Mating Envelope for an internal Feature of Size.
The center of the figure shows that the Unrelated Actual Envelope is the largest perfect cylinder that will fit inside the physical cylinder without regard to the datum. The Unrelated Actual Mating Envelope will almost never be perfectly perpendicular to the datum.
The right side of the figure shows that the Related Actual Mating Envelope is the largest perfect cylinder that is perpendicular to the datum and fits inside the physical cylinder. The Related Actual Mating Envelope is always perpendicular to the datum.
The size of the Unrelated Actual Mating Envelope is considered to be the size of the hole.
The axis of the Unrelated Actual Mating Envelope is considered to be the axis of the hole.
The center of the figure shows that the Unrelated Actual Envelope is the largest perfect cylinder that will fit inside the physical cylinder without regard to the datum. The Unrelated Actual Mating Envelope will almost never be perfectly perpendicular to the datum.
The right side of the figure shows that the Related Actual Mating Envelope is the largest perfect cylinder that is perpendicular to the datum and fits inside the physical cylinder. The Related Actual Mating Envelope is always perpendicular to the datum.
The size of the Unrelated Actual Mating Envelope is considered to be the size of the hole.
The axis of the Unrelated Actual Mating Envelope is considered to be the axis of the hole.