Datum Targets
As we discussed in the previous section, if we grab a dog's legs to hold him still, the dog gets claustrophobic and may bite us.
If we want to hold the dog in some exact position without the dog getting claustrophobic, we may want to use datum targets.
Datum targets are perfect, theoretical points or lines or areas that describe a gage.
We have discussed issues with the dog standing on the ground with four feet. If the dog were perfectly rigid, he would likely rock because only three feet would be in the same plane at any one time. We could instead describe three areas where three of the dog's feet could touch. Even a rigid statue of a dog standing on these three areas with three feet would be stable.
We would describe the size and shape of the areas. The areas would be located to each other with basic dimensions to indicate that theoretically they are perfectly located.
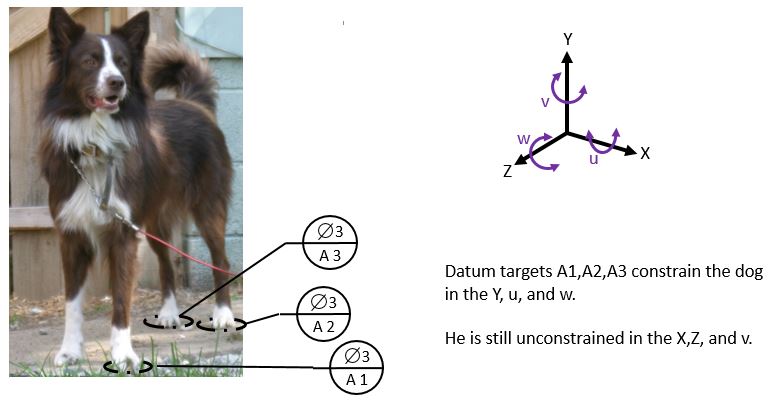
In the figure below, the dog is standing on three perfect 3 inch diameter disks. They are called out at datum targets A1, A2, and A3. The datum target symbols denote the datum target name in the bottom and the datum target diameter in the top.
On a drawing, the actual circle would be bounded by a phantom line and cross hatched.
The dog is holding his front right leg up off the ground a tiny bit in order to make sure he is oriented purely by the datum targets.
If we want to hold the dog in some exact position without the dog getting claustrophobic, we may want to use datum targets.
Datum targets are perfect, theoretical points or lines or areas that describe a gage.
We have discussed issues with the dog standing on the ground with four feet. If the dog were perfectly rigid, he would likely rock because only three feet would be in the same plane at any one time. We could instead describe three areas where three of the dog's feet could touch. Even a rigid statue of a dog standing on these three areas with three feet would be stable.
We would describe the size and shape of the areas. The areas would be located to each other with basic dimensions to indicate that theoretically they are perfectly located.
In the figure below, the dog is standing on three perfect 3 inch diameter disks. They are called out at datum targets A1, A2, and A3. The datum target symbols denote the datum target name in the bottom and the datum target diameter in the top.
On a drawing, the actual circle would be bounded by a phantom line and cross hatched.
The dog is holding his front right leg up off the ground a tiny bit in order to make sure he is oriented purely by the datum targets.
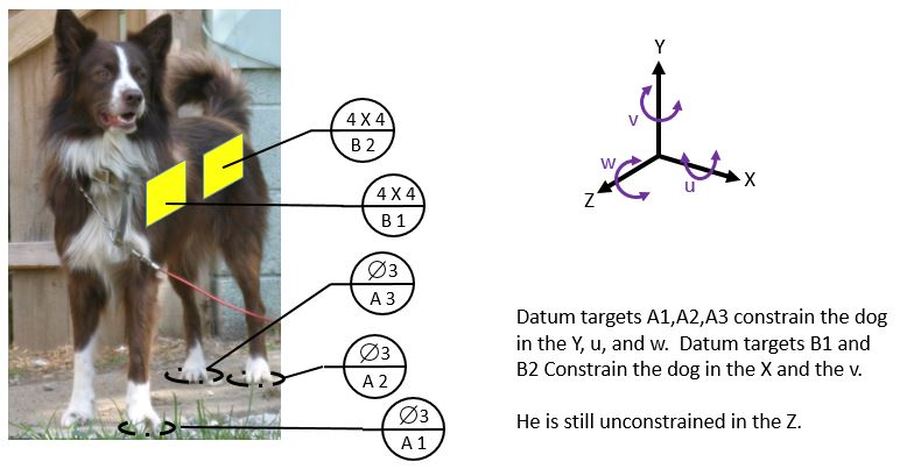
Now we establish two perfectly flat squares, each exactly 4 inches square, and each perfectly located. They are also perfectly in line with each other and perfectly perpendicular to the plane established by datum targets A1, A2, and A3. The dog leans against them. These are datum targets B1 and B2. They constrain the dog in the X translation and the v rotation. Now the dog can no longer move side to side or chase his tail. But he can still move fore-aft in the Z translation.
Note that the notation for the B datums starts with B1 so that we have B1 and B2. It's not B4 and B5.
Note that the notation for the B datums starts with B1 so that we have B1 and B2. It's not B4 and B5.
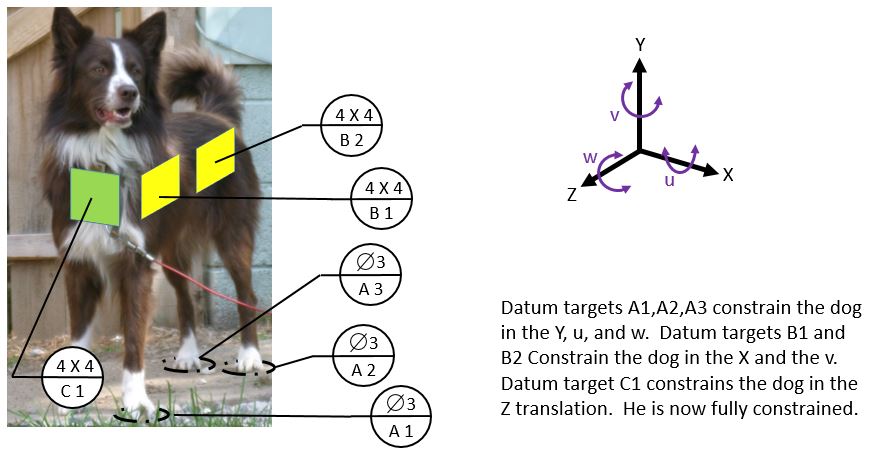
We establish one more perfectly flat square, exactly 4 inches square, perfectly located, and exactly perpendicular to the plane formed by A1, A2, and A3 and the plane formed by B1 and B2. The dog leans against C1 while standing on A1,A2, and A3 and still leaning against B1 and B2. The dog is now fully constrained, and we can measure features on the dog relative to the datum targets.
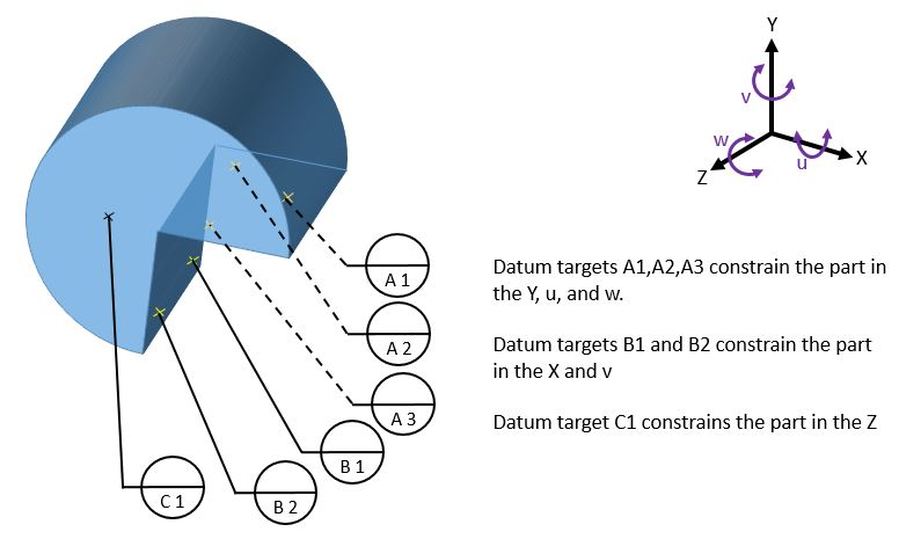
Consider the part below with datum target points. Datum target points A1,A2, and A3 contact a surface of the part that is hidden in this view. They constrain the part in the Y translation and in the u and w rotations.
Datum target points B1 and B2 contact the surface that faces to the right. They constrain the part in the X translation and the v rotation.
That leaves datum target point C1 to constrain the part in the Z translation.
Thus the part is fully constrained.
Datum target points B1 and B2 contact the surface that faces to the right. They constrain the part in the X translation and the v rotation.
That leaves datum target point C1 to constrain the part in the Z translation.
Thus the part is fully constrained.