Feature Of Size Datums
Consider the dog again. When he is standing on the ground, the ground determines where he will be in the vertical direction. So he is restrained in the vertical direction. If he keeps his feet on the ground, he will also be unable to roll over or do a somersault. So he is also constrained in two rotations. The ground acts as a primary datum.
The dog can still go fore-aft and side to side and spin around (chase his tail). So that's two translations and one rotation that still need to be constrained.
The dog can still go fore-aft and side to side and spin around (chase his tail). So that's two translations and one rotation that still need to be constrained.
Now if we grab one of the dog's legs, if he will stand for it, he is no longer able to move fore-aft or side to side. He can still rotate around the leg that we are holding. So we have constrained two additional translations and still have one rotation unconstrained. Remember that the dog's leg is a feature of size. So when we grab the dog's leg, it acts as a feature of size datum. So now we have the ground as a primary datum (which in this case is a planar datum) and the leg is a secondary datum.
If we grab a second leg, it will constrain the dog in the final rotation and all degrees of freedom will be constrained. The dog will probably feel claustrophobic and bite us.
Regardless of whether or not we get bit, the ground is the primary datum, the first leg is the secondary datum, and the third leg is the tertiary datum (which in this case is another feature of size datum).
Regardless of whether or not we get bit, the ground is the primary datum, the first leg is the secondary datum, and the third leg is the tertiary datum (which in this case is another feature of size datum).
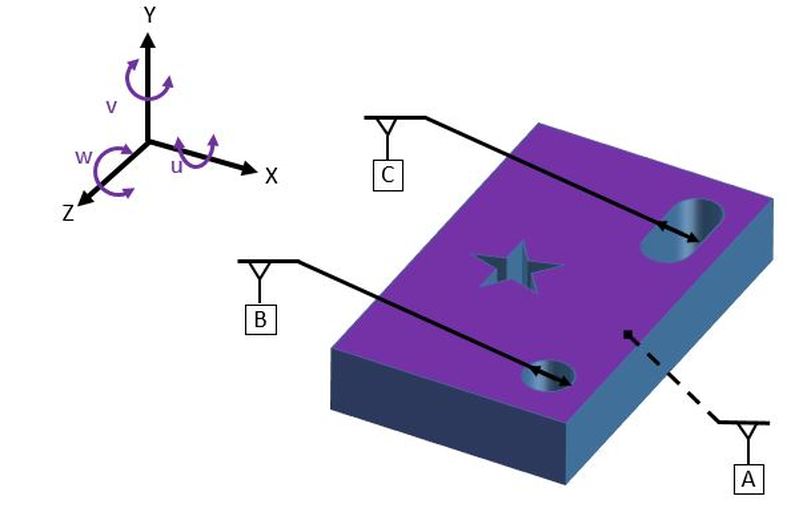
We can do the same thing with parts that are not dogs. In the block below, we will want to measure the star's location relative to the hole and the slot. We will set up our datums as shown below. Datum feature A is the bottom surface of the block. Datum feature B is the hole. Datum feature C is the width of the slot.
In this case we will make datum A primary, datum B secondary, and datum C tertiary. Let's look at how this works and how this datum scheme restrains all of the degrees of freedom.
In this case we will make datum A primary, datum B secondary, and datum C tertiary. Let's look at how this works and how this datum scheme restrains all of the degrees of freedom.
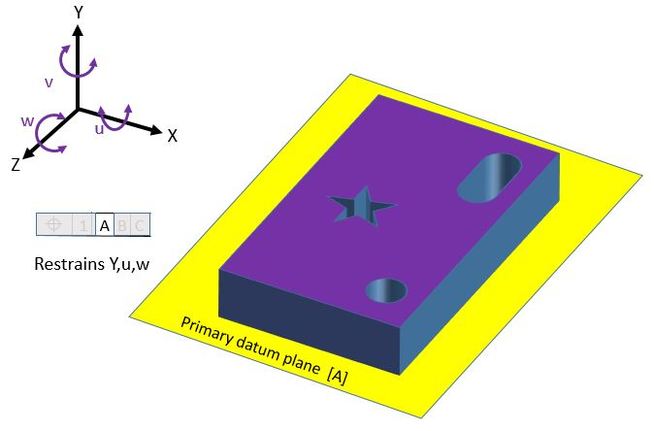
We start out needing to keep the star and the hole and the slot nice and perpendicular to the bottom of the part. So we make the bottom of the part our primary datum. This orients everything on the part relative to the bottom of the part.
Datum Plane A restrains the Y translation and the u and w rotations.
Datum Plane A restrains the Y translation and the u and w rotations.
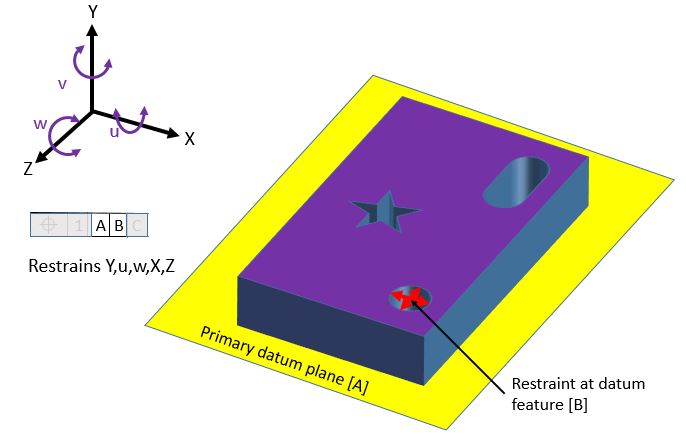
Now we will add datum hole B. We picture it with the four pronged arrow because we will restrain it with something that constrains it in the directions indicated by the arrows.
Datum hole B adds constraints in the X and Z directions. The only degree of freedom left unconstrained is the v rotation. In this case the part can still rotate around the axis of the hole.
Datum hole B adds constraints in the X and Z directions. The only degree of freedom left unconstrained is the v rotation. In this case the part can still rotate around the axis of the hole.
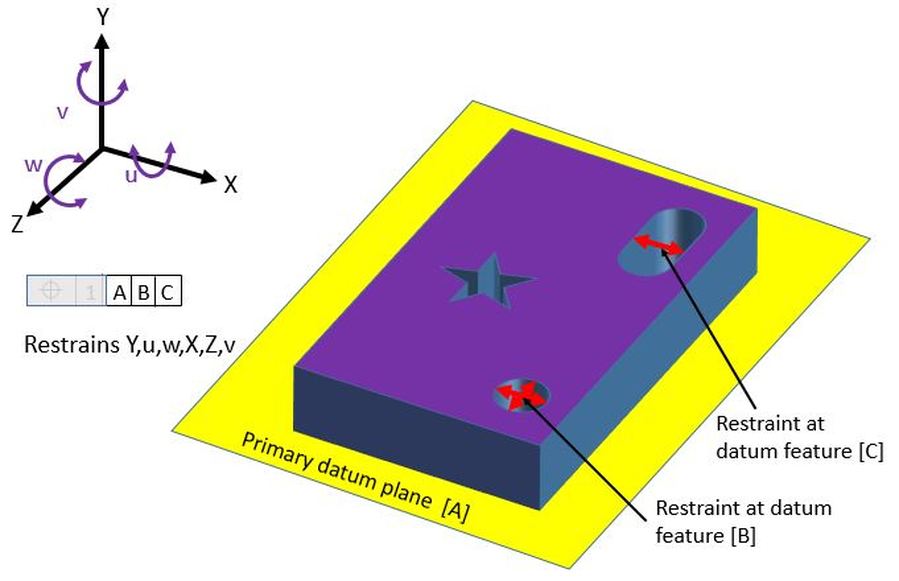
Now we add datum slot C. Once again the red arrows indicate the direction that will be constrained. We can see that this will stop the rotation around the axis of the hole, thereby constraining the part in the v rotation.
The part is now fully constrained, and we can make our measurements.
The part is now fully constrained, and we can make our measurements.