Features and Features Of Size
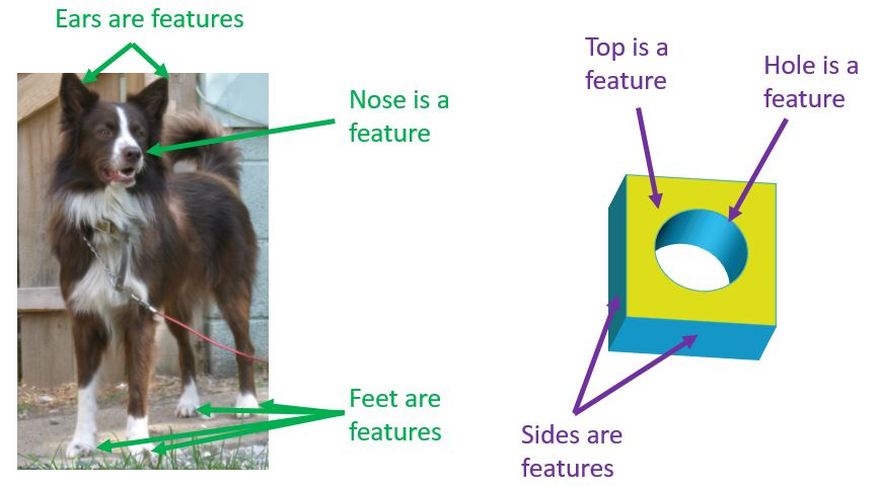
Everything is comprised of Features. Each part of the dog is a feature, as the figure below shows. Also on engineering parts, each thing we can point to on it is a feature as shown below.
But note that features are always things that we can touch. So the hole (at its surface) is a feature. The axis of the hole is not a feature. Likewise a slot is a feature, but the center-plane of the slot is not a feature.
But note that features are always things that we can touch. So the hole (at its surface) is a feature. The axis of the hole is not a feature. Likewise a slot is a feature, but the center-plane of the slot is not a feature.
Some features are special. We call them Features Of Size. Features of size are useful to us because there are things that we can do with features of size that we cannot do with things that are not features of size. We will find out about the special things we can do with features of size in future sections.
Features Of Size are divided into Regular Features Of Size and Irregular Features Of Size. First we will discuss Regular Features Of Size. They are by far the most common.
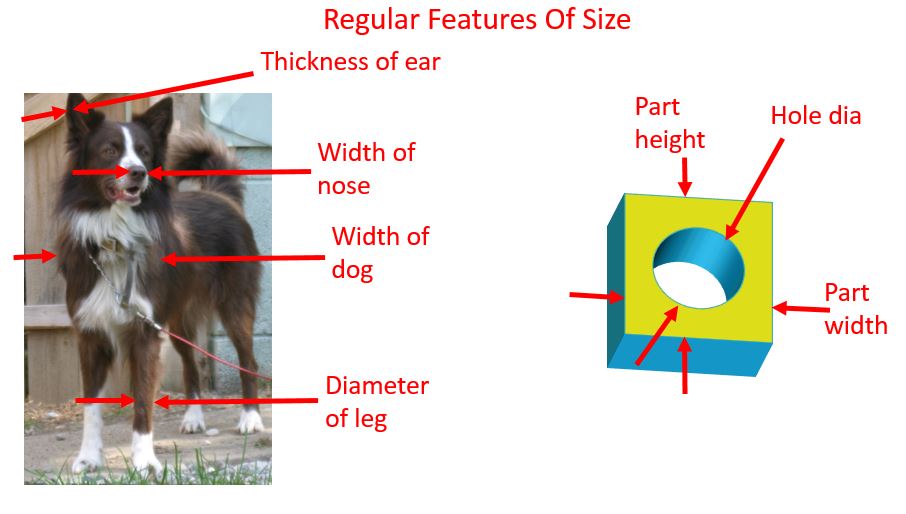
A Regular Feature Of size is one that has a size associated with it (a diameter or a width or a length or a thickness). The special thing about a Regular Feature Of Size that makes it regular is the fact that it has Opposed Surfaces. That means, as shown in the figure below, that if we indicate the size with a couple of arrows that point at each other, the feature touches both of the arrows.
When we measure the thickness of the dog's ear, the arrows pointing at each other touch both sides of the ear. The same is true for the width of the nose, the width of the dog, and the diameter of the leg.
Likewise for the block with the hole in it, the arrows pointing at each other touch the width and the height. It is the same for the surface of the hole.
Features Of Size are divided into Regular Features Of Size and Irregular Features Of Size. First we will discuss Regular Features Of Size. They are by far the most common.
A Regular Feature Of size is one that has a size associated with it (a diameter or a width or a length or a thickness). The special thing about a Regular Feature Of Size that makes it regular is the fact that it has Opposed Surfaces. That means, as shown in the figure below, that if we indicate the size with a couple of arrows that point at each other, the feature touches both of the arrows.
When we measure the thickness of the dog's ear, the arrows pointing at each other touch both sides of the ear. The same is true for the width of the nose, the width of the dog, and the diameter of the leg.
Likewise for the block with the hole in it, the arrows pointing at each other touch the width and the height. It is the same for the surface of the hole.
By contrast, the things in the figure below are not regular features of size. In fact, they are not features of size at all. Measuring from ear to foot, the arrows do not line up with each other. The same is true of the height of the dog. The arrows go from the ground to the dog’s back – or from the bottom of the dog’s foot to his back. The dog’s height is not contained by two arrows pointing at each other.
Also for the part on the right, the distance from the bottom to the surface on the left side of of the part has one arrow in the part and the other one hanging out in space. Also the depth of the slot on the right has one arrow in the part and the other one hanging out in space.
Also for the part on the right, the distance from the bottom to the surface on the left side of of the part has one arrow in the part and the other one hanging out in space. Also the depth of the slot on the right has one arrow in the part and the other one hanging out in space.
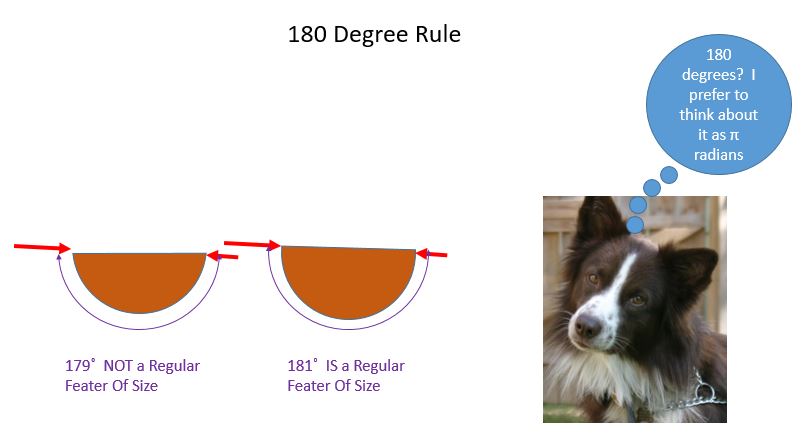
The figure below shows the 180 degree rule. Circles and spheres are regular features of size, and things that are almost circles and almost spheres are regular features of size also. As long as it's possible to find a place where there is circle or sphere touching both of the arrows, it's a regular feature of size. So as long as it's 180 degrees or more, it's a regular feature of size. But if it's less then 180 degrees, then one of the arrows is hanging out in space. Then it's not a regular feature of size.
There are things that we can do with features of size that we want to do with things that are not regular features of size. So Irregular features of size were created. Irregular features of size enable us to do some of the cool feature of size things with shapes that are not regular features of size.
Irregular features of size come in two varieties - type A and type B.
Type A irregular features of size are shapes that can nicely fit into a sphere or circle or between two parallel planes. The example on the left is a triangular shape that fits nicely within a circle. The example on the right is a shape that fits nicely between two parallel planes. Note that in both cases these do not qualify as regular features of size.
A type B irregular feature of size is a shape that does not nicely fit into a sphere or between two parallel planes. Note the example below.
In both cases, there is a special way to tolerance them and special things we can do with them as we treat them as features of size. We will develop these in future sections.
Irregular features of size come in two varieties - type A and type B.
Type A irregular features of size are shapes that can nicely fit into a sphere or circle or between two parallel planes. The example on the left is a triangular shape that fits nicely within a circle. The example on the right is a shape that fits nicely between two parallel planes. Note that in both cases these do not qualify as regular features of size.
A type B irregular feature of size is a shape that does not nicely fit into a sphere or between two parallel planes. Note the example below.
In both cases, there is a special way to tolerance them and special things we can do with them as we treat them as features of size. We will develop these in future sections.