Applying RSS to a two column stack
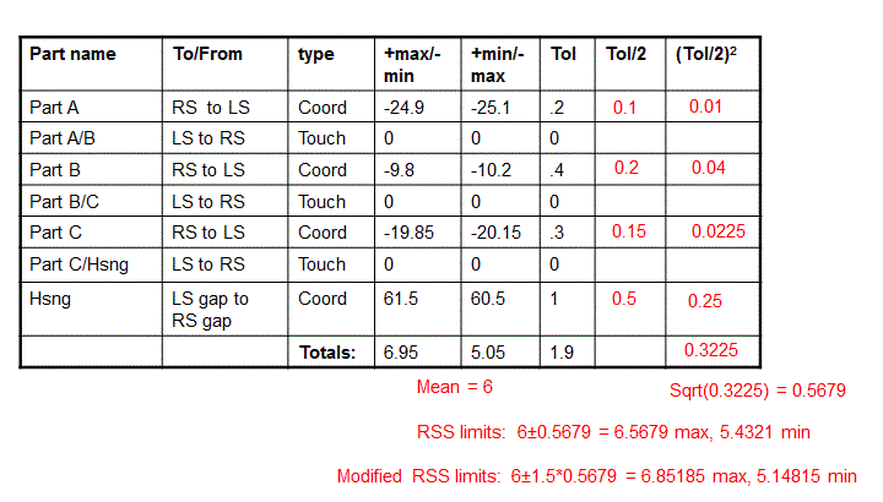
This is the simplest case of applying RSS to a two column stack. See the figure below. The numbers in black are the limit stack. The numbers in red are the calculations for RSS.
For RSS, we need a mean and a plus and minus. We get the mean by averaging the Max and Min columns from the limit stack. This gives us our mean of 6.
To get our plus and minus values, we turn to the Tol column. For each line in the stack that represents an independent variable, divide that Tol value by two and place the value in the Tol/2 column. Then square each of the Tol/2 values and place the value in the far right column. Add up the values in the right column. This total is the plus and minus value. So our straight RSS stack is 6 plus or minus 0.5679.
If we choose to use a safety factor, we multiply our plus and minus value by the safety factor. In this case we chose a safety factor of 1.5. So we multiply the 0.5679 by 1.5 to give us an RSS stack with 1.5 safety factor of 6 plus or minus 0.85185.
This is the simplest case of applying RSS to a two column stack. See the figure below. The numbers in black are the limit stack. The numbers in red are the calculations for RSS.
For RSS, we need a mean and a plus and minus. We get the mean by averaging the Max and Min columns from the limit stack. This gives us our mean of 6.
To get our plus and minus values, we turn to the Tol column. For each line in the stack that represents an independent variable, divide that Tol value by two and place the value in the Tol/2 column. Then square each of the Tol/2 values and place the value in the far right column. Add up the values in the right column. This total is the plus and minus value. So our straight RSS stack is 6 plus or minus 0.5679.
If we choose to use a safety factor, we multiply our plus and minus value by the safety factor. In this case we chose a safety factor of 1.5. So we multiply the 0.5679 by 1.5 to give us an RSS stack with 1.5 safety factor of 6 plus or minus 0.85185.