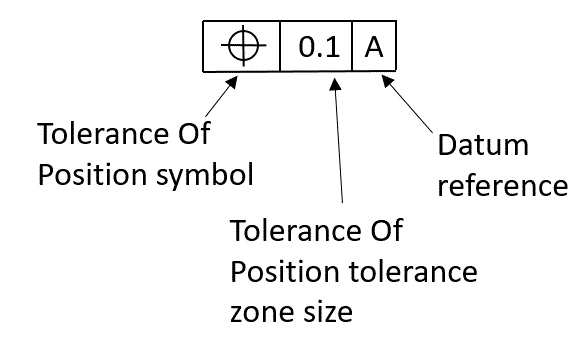
Tolerance Of Position
The feature control frame for Tolerance Of Position is shown below:
This chapter is about Tolerance Of Position. It is not about True Position Tolerance. True Position is a perfect, theoretical location that is usually denoted by Basic Dimensions. Tolerance Of Position is a geometric control that specifies how far away from True Position a feature of size is allowed to be.
Tolerance Of Position has some fundamental rules:
1. Tolerance Of Position must always be applied to a Feature of Size
2. Tolerance Of Position must always be located by Basic Dimensions. The Basic Dimensions may be explicitly called out or implied.
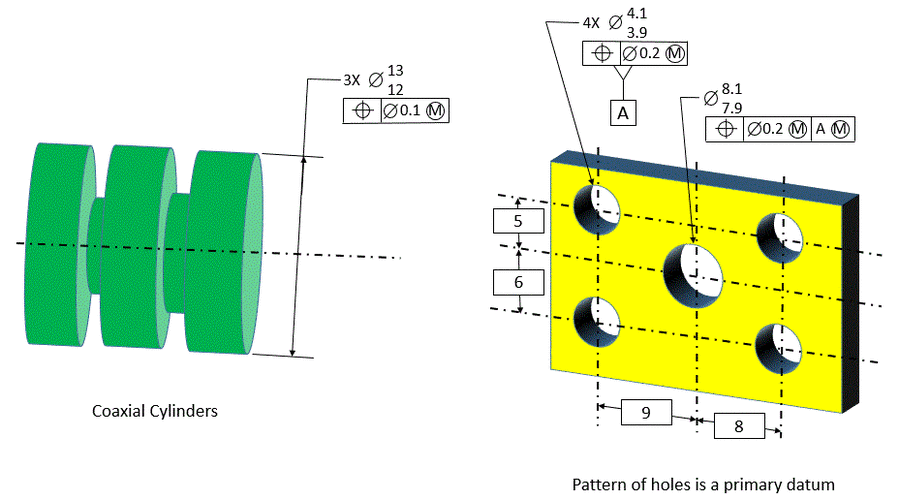
3. Tolerance Of Position must always have one or more datum references except for two exceptions: Coaxial cylinders and a pattern of features of size used as a primary datum.
Tolerance Of Position has some fundamental rules:
1. Tolerance Of Position must always be applied to a Feature of Size
2. Tolerance Of Position must always be located by Basic Dimensions. The Basic Dimensions may be explicitly called out or implied.
3. Tolerance Of Position must always have one or more datum references except for two exceptions: Coaxial cylinders and a pattern of features of size used as a primary datum.
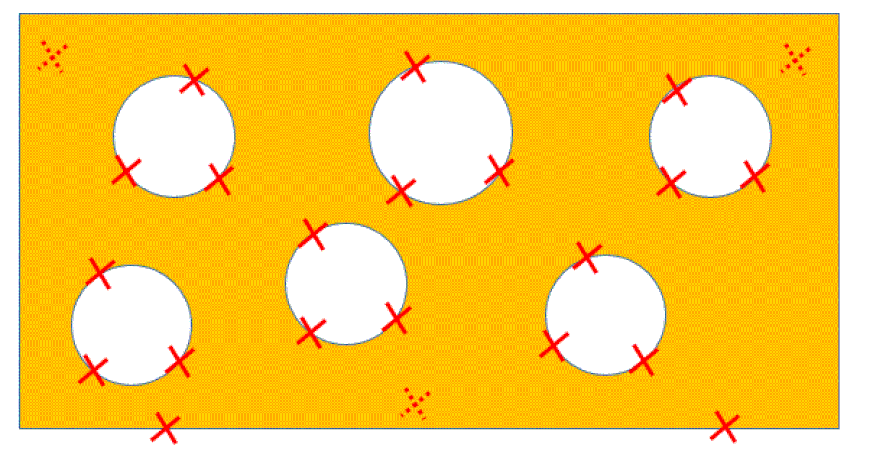
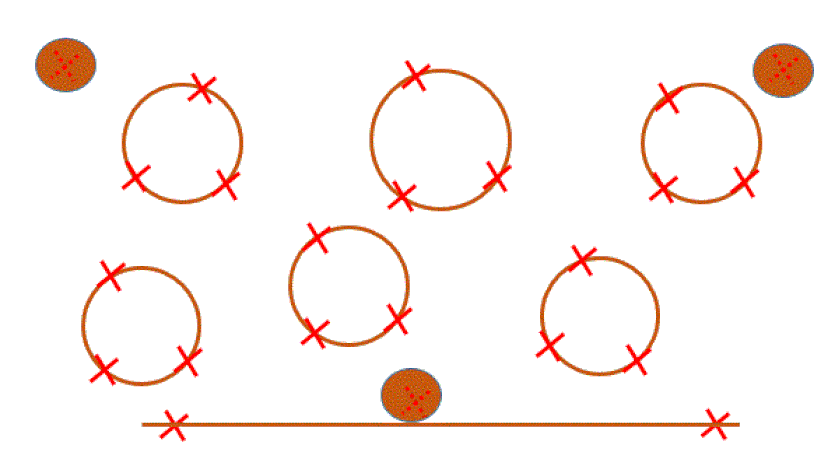
The figure below shows the two cases in which a Tolerance Of Position does not require a datum reference. On the left, we have three coaxial cylinders. They are located relative to each other, not relative to anything else.
On the right, the pattern of four holes is a primary datum. This is an unusual situation, but it is possible. The tolerance of position locates the holes within the pattern relative to each other. The large hole in the middle of the part is then located relative to the pattern of four holes. Therefore the large hole in the center does require a datum reference.
On the right, the pattern of four holes is a primary datum. This is an unusual situation, but it is possible. The tolerance of position locates the holes within the pattern relative to each other. The large hole in the middle of the part is then located relative to the pattern of four holes. Therefore the large hole in the center does require a datum reference.
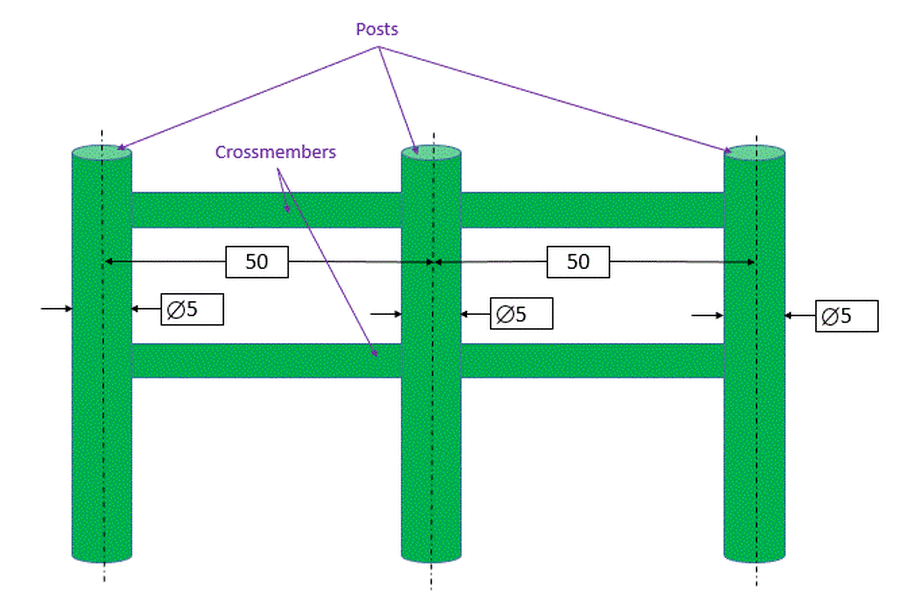
For our discussion of Tolerance Of Position, we will first look at our holes that we are digging for fence posts to keep our dog in our yard.
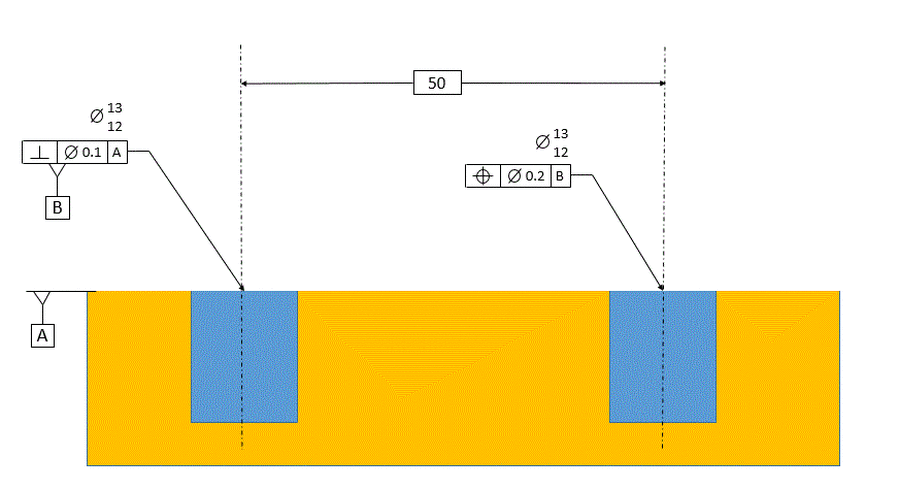
In previous chapters we talked about the orientation of the holes, but we never talked about the location of the holes. In the figure below, the hole on the right is located relative to the hole on the left. Note the addition of a basic dimension and a tolerance of position control.
In order to understand our tolerance of position control, we must thoroughly understand our datum.
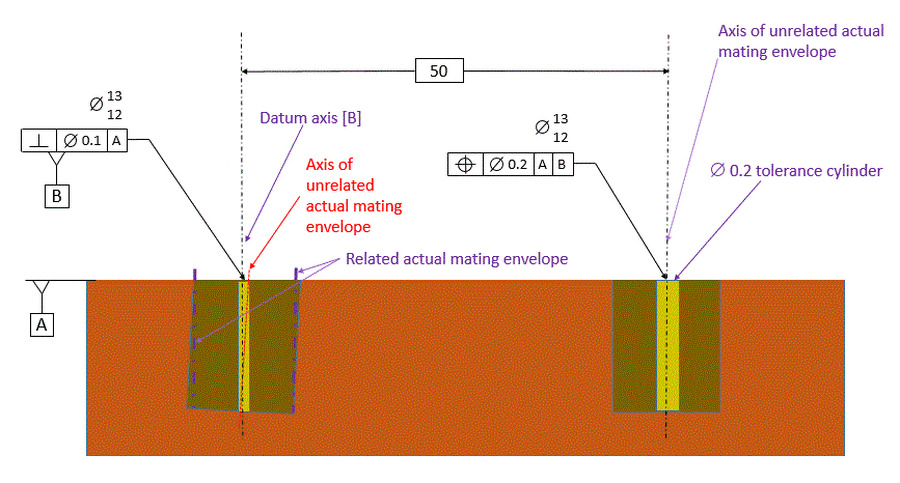
For now, focus on the datum hole. We must establish datum axis [B]. The hole on the right will be located relative to datum axis [B]. Our datum callouts in the feature control frame for the Tolerance Of Position tells us that datum [B] must be perpendicular to datum [A].
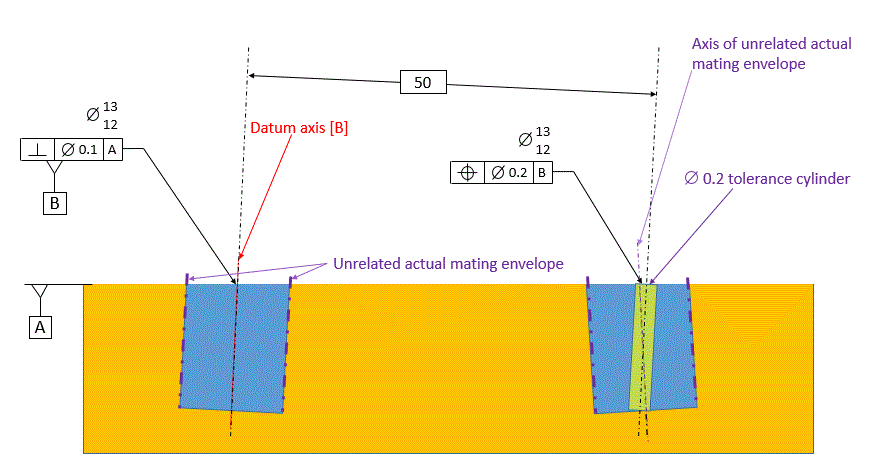
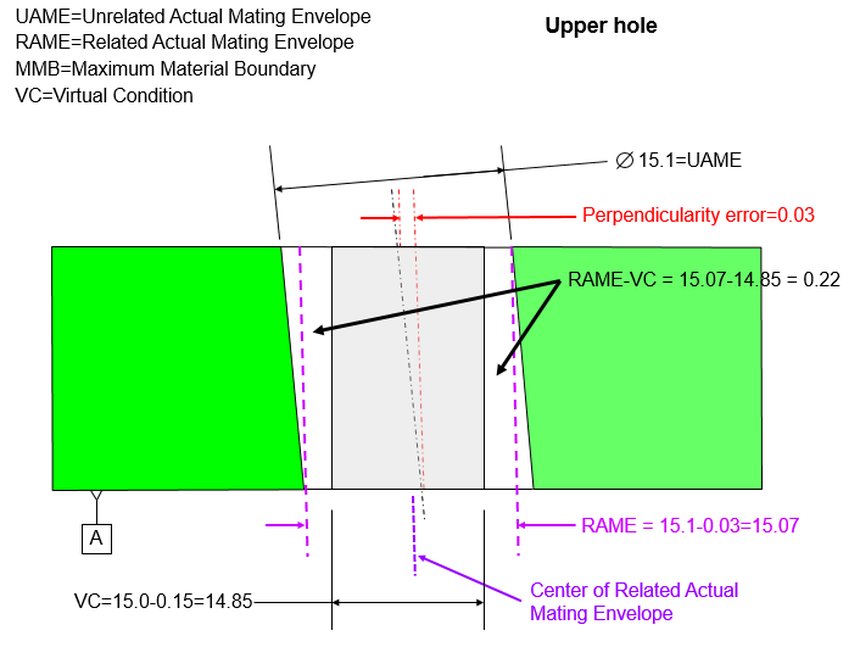
The datum hole is not necessarily perpendicular to datum [A]. The datum hole has a perpendicularity control that controls the orientation of the datum hole. The perpendicularity control says that there is a tolerance cylinder that is 0.1 diameter that is exactly perpendicular to datum [A]. The axis of the unrelated actual mating envelope of the datum hole must fall within this tolerance cylinder.
The axis of the unrelated actual mating envelope cannot be datum [B] because this axis is not necessarily perpendicular to datum [A]. Datum [B] is the axis of the Related Actual Mating Envelope of the datum hole. The Related Actual Mating Envelope is the largest perfect cylinder that is exactly perpendicular to datum [A] and still fits within the datum hole.
In previous chapters we talked about the orientation of the holes, but we never talked about the location of the holes. In the figure below, the hole on the right is located relative to the hole on the left. Note the addition of a basic dimension and a tolerance of position control.
In order to understand our tolerance of position control, we must thoroughly understand our datum.
For now, focus on the datum hole. We must establish datum axis [B]. The hole on the right will be located relative to datum axis [B]. Our datum callouts in the feature control frame for the Tolerance Of Position tells us that datum [B] must be perpendicular to datum [A].
The datum hole is not necessarily perpendicular to datum [A]. The datum hole has a perpendicularity control that controls the orientation of the datum hole. The perpendicularity control says that there is a tolerance cylinder that is 0.1 diameter that is exactly perpendicular to datum [A]. The axis of the unrelated actual mating envelope of the datum hole must fall within this tolerance cylinder.
The axis of the unrelated actual mating envelope cannot be datum [B] because this axis is not necessarily perpendicular to datum [A]. Datum [B] is the axis of the Related Actual Mating Envelope of the datum hole. The Related Actual Mating Envelope is the largest perfect cylinder that is exactly perpendicular to datum [A] and still fits within the datum hole.
Having established our datums, we can now look at how the tolerance of position locates and orients the hole relative to the datums.
The tolerance of position callout tells us that there is a tolerance zone cylinder that is 0.2 diameter. This cylinder is exactly perpendicular to datum [A], and the center of this cylinder is exactly 50 from datum [B]. The axis of the unrelated actual mating envelope of the hole must fall within this tolerance cylinder.
We can see from the figure below that the requirement for the axis of the unrelated actual mating envelope falling within this cylinder allows the hole to move 0.1 toward datum [B] or 0.1 away from datum [B] relative to its ideal position. The requirement also allows the hole to tilt relative to datum [A] with the tilting being restricted by the axis of the unrelated actual mating envelope staying within the tolerance cylinder.
The tolerance of position callout tells us that there is a tolerance zone cylinder that is 0.2 diameter. This cylinder is exactly perpendicular to datum [A], and the center of this cylinder is exactly 50 from datum [B]. The axis of the unrelated actual mating envelope of the hole must fall within this tolerance cylinder.
We can see from the figure below that the requirement for the axis of the unrelated actual mating envelope falling within this cylinder allows the hole to move 0.1 toward datum [B] or 0.1 away from datum [B] relative to its ideal position. The requirement also allows the hole to tilt relative to datum [A] with the tilting being restricted by the axis of the unrelated actual mating envelope staying within the tolerance cylinder.
The fact that tolerance of position allows some tilting should not be ignored. Recall that the purpose of these holes is to plant fence posts in them for our fence that will keep the dog in the yard. See the figure below that includes the fence posts. The fence will be okay with the fence post on the right being out of position to the extent allowed by the tolerance of position. However, the tilting has a geometric effect. This geometric effect will allow the top of the fence post to move much more than is acceptable.
In order to get our fence post to do what we want it to do, we will use the Projected Tolerance Zone modifier. The Projected Tolerance Zone modifier is the letter P in the circle in the feature control frame. The Projected Tolerance Zone modifier specifies that the tolerance zone is projected above the part. It is no longer inside the part. It is completely above the part. The number after Projected Tolerance Zone modifier in the circle is the distance above the part that we want the tolerance zone projected. In our case, our posts will stick above the ground a distance of 40. Therefore we want to project our tolerance zone 40 above the part.
Now the axis of the unrelated actual mating envelope of the hole, and therefore the axis of the post, must stay within this tolerance zone that is above the part. This limits the tilting of the post that is allowed. It restricts the movement of the top of the post to an amount that is acceptable.
Now the axis of the unrelated actual mating envelope of the hole, and therefore the axis of the post, must stay within this tolerance zone that is above the part. This limits the tilting of the post that is allowed. It restricts the movement of the top of the post to an amount that is acceptable.
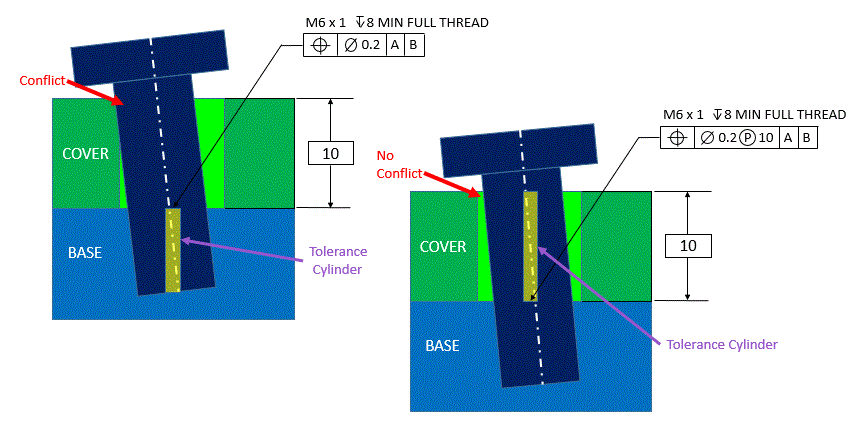
The figure below shows the classic example of projected tolerance zone. On the left, the tolerance cylinder is inside the part. The bolt centers itself on the threads in the threaded hole. As the bolt extends through the cover while tilted as much as the tolerance of position will allow, there is a conflict between the bolt and the side of the clearance hole in the cover.
On the right, the tolerance zone is projected from the top of the base to the top of the cover. The axis of the hole, and therefore the axis of the bolt, stays within the tolerance cylinder as it goes through the clearance hole in the cover and there is no conflict between the bolt and the side of the clearance hole in the cover.
On the right, the tolerance zone is projected from the top of the base to the top of the cover. The axis of the hole, and therefore the axis of the bolt, stays within the tolerance cylinder as it goes through the clearance hole in the cover and there is no conflict between the bolt and the side of the clearance hole in the cover.
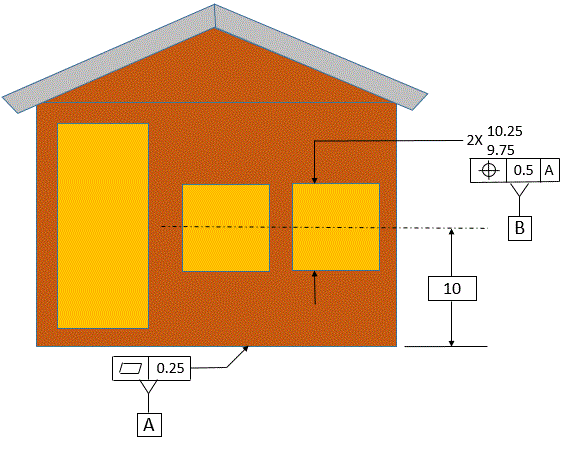
Now let's look at locating some windows in our dog house. To simplify things, we will only look at locating them vertically. The windows are features of size, so we can locate them with a tolerance of position. We will dimension them as a pattern.
The tolerance of position tells us that exactly 10 above datum [A], there is a perfect plane. Centered on that plane are two parallel planes that are 0.5 apart. The center planes of the unrelated actual mating envelopes of the window heights must fall between these two parallel planes. Note that since the tolerance zone is two parallel planes and not a cylinder, the diameter symbol is not used in the feature control frame.
The tolerance of position tells us that exactly 10 above datum [A], there is a perfect plane. Centered on that plane are two parallel planes that are 0.5 apart. The center planes of the unrelated actual mating envelopes of the window heights must fall between these two parallel planes. Note that since the tolerance zone is two parallel planes and not a cylinder, the diameter symbol is not used in the feature control frame.
Since each window could be at the opposite end of the tolerance zone, the windows could be offset from each other. The windows can also rotate relative to datum [A] and relative to each other.
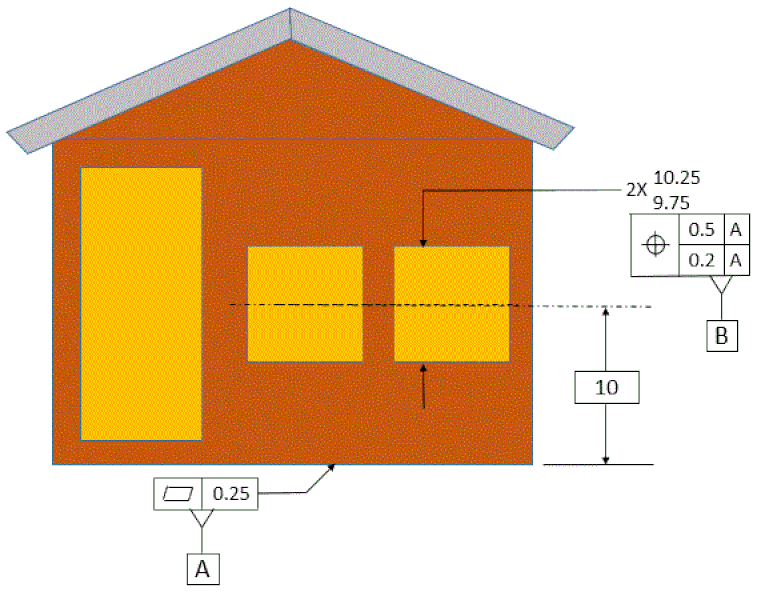
We would like to tighten up the alignment between the windows and the orientation relative to datum [A]. We do not need to tighten the location of the pattern relative to [A]. We will use a composite tolerance. The composite tolerance has two or more lines that share a single tolerance of position symbol. The composite tolerance is always applied to a pattern of features of size. The top line controls the location of the pattern. The bottom line controls orientation and alignment and/or spacing within the pattern, never location of the pattern. Note that since the bottom line controls orientation and not location, we are allowed to have the same datums in the same order in the bottom line as in the top line.
The top line controls the position of the pattern within the same 0.5 tolerance zone as the simple tolerance of position. The bottom line holds the center planes of both windows within the red tolerance zone. The red tolerance zone is two parallel planes that are 0.2 apart. This tolerance zone is exactly parallel to datum [A], but this tolerance zone is allowed to float within the 0.5 tolerance zone. It aligns the two windows with each other and controls the orientation to [A] while allowing the location of the pattern to vary within the 0.5 tolerance zone.
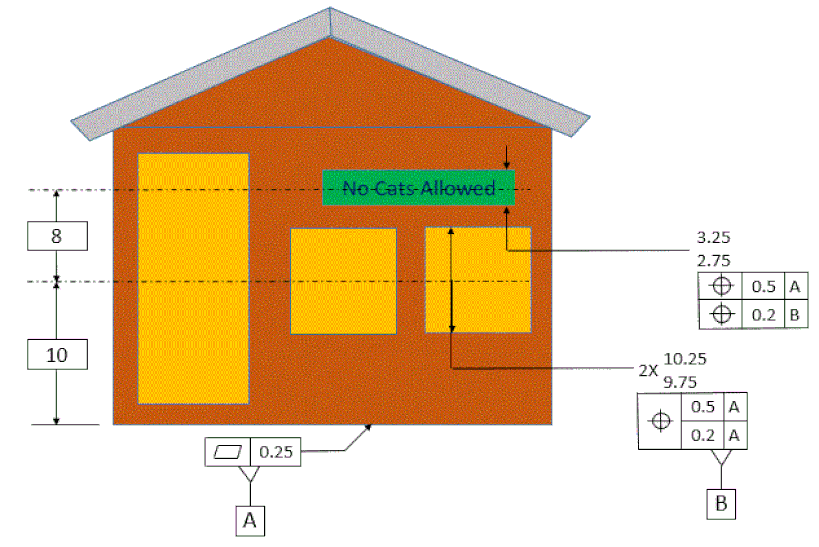
Now we want to mount a sign on our dog house. The sign’s location relative to datum [A] is not critical. However, we want to make sure that the sign is located and oriented tightly relative to the windows. Therefore we use a multiple single segment position tolerance.
The multiple single segment tolerance consists of multiple tolerance of position feature control frames stacked on each other. Each line is an independent requirement.
The multiple single segment tolerance consists of multiple tolerance of position feature control frames stacked on each other. Each line is an independent requirement.
The center plane of the unrelated actual mating envelope of the sign must fall within the red tolerance zone. The red tolerance zone is 0.2 wide and is exactly parallel and exactly located to datum [B]. The red tolerance zone can float within the blue tolerance zone which is exactly oriented and located to datum [A]. The effect is that as the windows move up and down, the sign follows them and stays located and oriented to the windows.
The multiple single segment tolerance is very flexible. The only requirement is that the datums in a lower segment must not be exact repeats of the datums in the upper segment. That would cause a conflict.
The multiple single segment tolerance is very flexible. The only requirement is that the datums in a lower segment must not be exact repeats of the datums in the upper segment. That would cause a conflict.
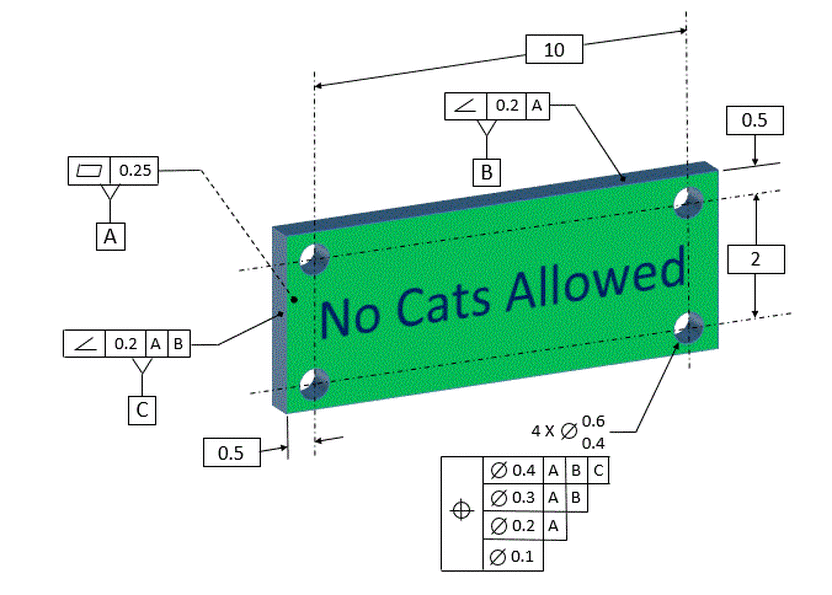
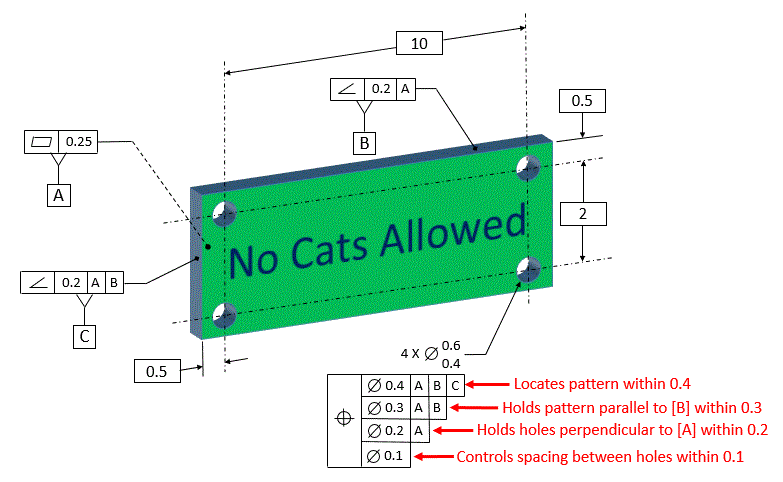
Now let's take a closer look at the detail of the sign that we want to attach over the windows. The sign with be attached with four screws, so we need four clearance holes in the sign. The location of the holes in the sign is not critical. However, we want the holes lined up nicely with the top edge of the sign so that the sign does not end up being crooked. We also want to have the holes nicely square to the back of the part, and we want the spacing of the holes carefully controlled.
We accomplish all of this with a composite tolerance as shown below.
The sign is dimensioned with datum [A] being the back of the part. Datum [B] is the top surface, and datum [C] is the left side. The holes are located with basic dimensions, and the composite tolerance locates and orients the holes.
We accomplish all of this with a composite tolerance as shown below.
The sign is dimensioned with datum [A] being the back of the part. Datum [B] is the top surface, and datum [C] is the left side. The holes are located with basic dimensions, and the composite tolerance locates and orients the holes.
Since location if the pattern of holes is not as critical as orientation, the top line of the composite tolerance locates the pattern of holes within 0.4.
The second line holds the pattern of holes parallel to the top so that the sign will not end up being tilted. It controls the parallelism between the pattern of holes and the top surface within 0.3.
The third line holds the holes square to the back of the part within 0.2
The fourth line has no datum, therefore it just controls the spacing of the parts within the pattern.
The second line holds the pattern of holes parallel to the top so that the sign will not end up being tilted. It controls the parallelism between the pattern of holes and the top surface within 0.3.
The third line holds the holes square to the back of the part within 0.2
The fourth line has no datum, therefore it just controls the spacing of the parts within the pattern.
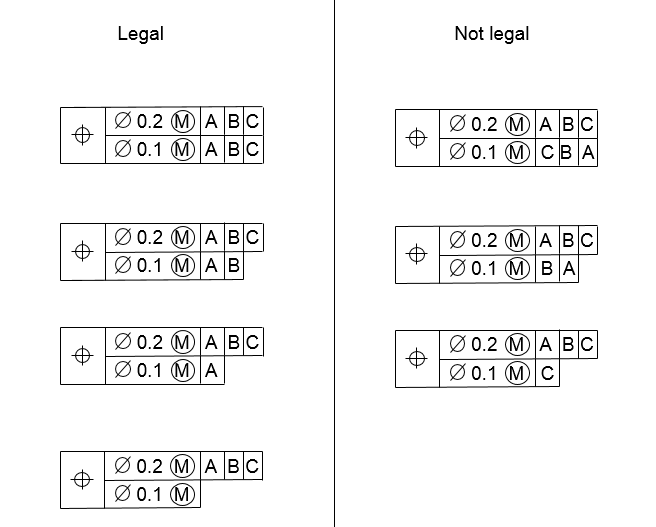
Note that as we go from top to bottom, the second line could have either exactly the same datum references as the top line or a subset. The third and fourth lines must have datum references that are subsets of the line above, and the datums must always be in the same order as the line above.
The only issue left now is to break the news to the cat that she is not allowed in the dog house.
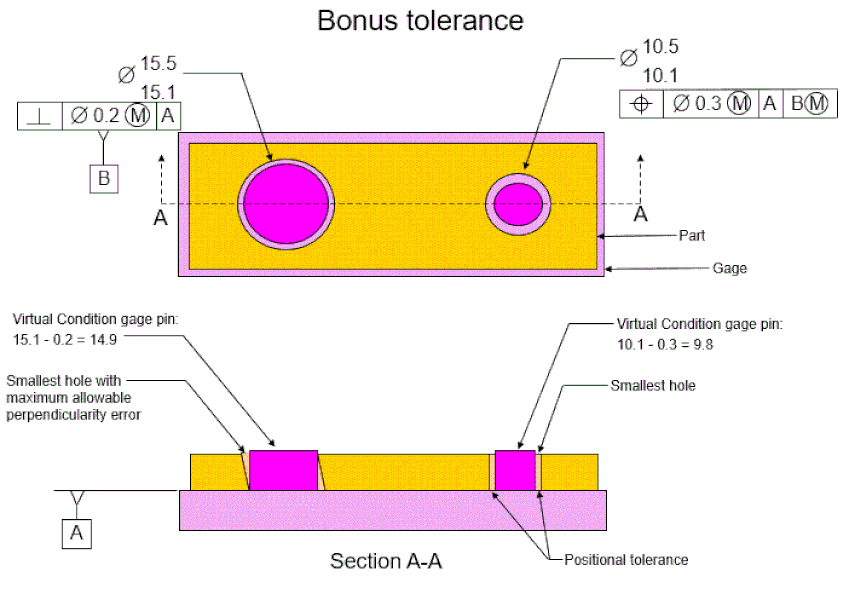
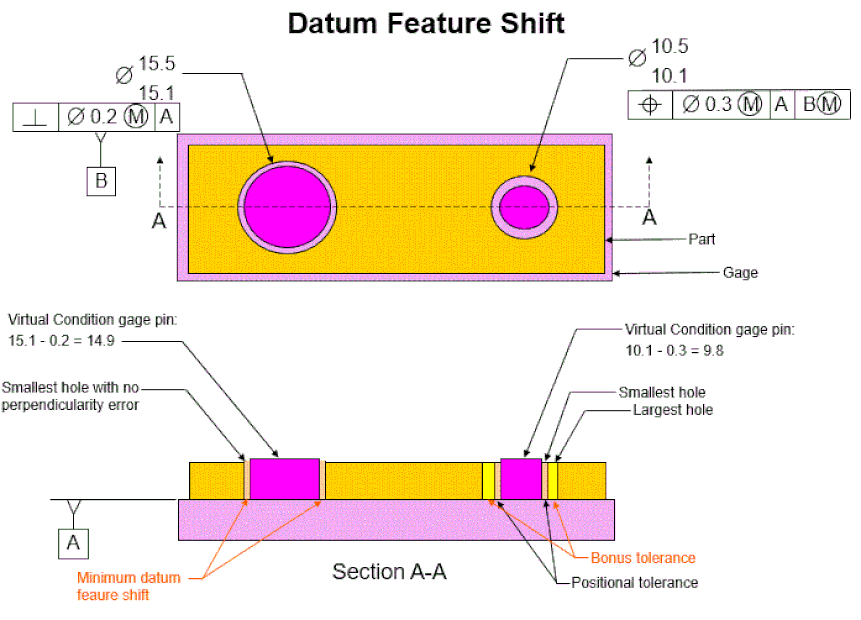
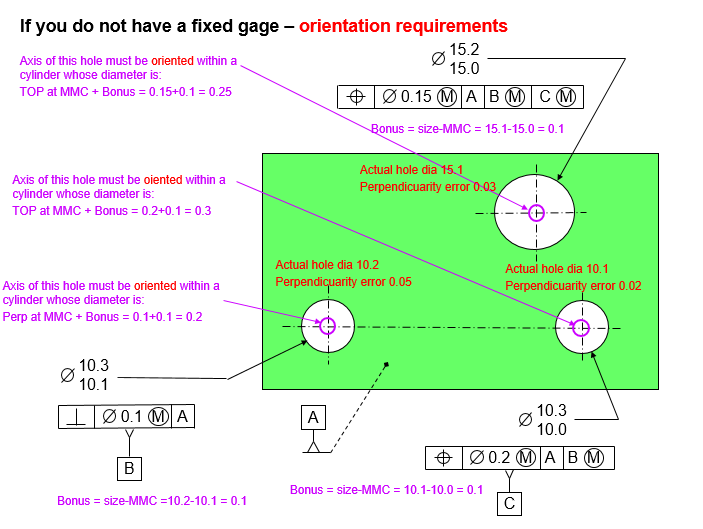
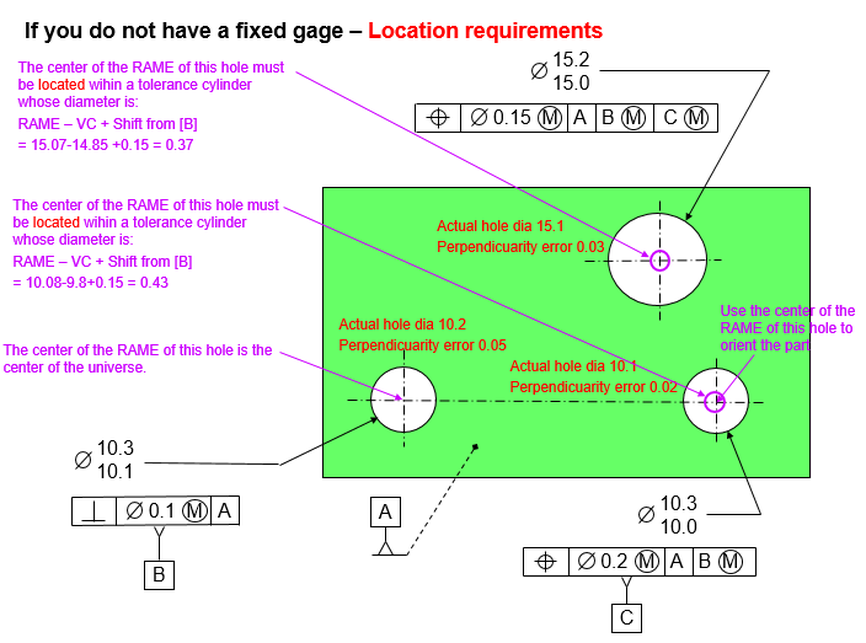
To understand bonus tolerance, look at how the part fits on the gage.
The hole on the right, the one that is not the datum, is called the ‘considered’ hole. In order to fit on the gage, the smallest considered hole must fit over the gage pin when the hole has position error equal to its positional tolerance.
The pin that the hole must fit over needs to be at its virtual condition – the smallest hole minus the positional tolerance value.
The hole on the left is the datum feature. The gage pin at the datum feature must be small enough for the smallest datum hole to fit over the pin when the datum hole has its maximum allowable perpendicularity error. Therefore the gage pin for the datum feature must be equal to the datum feature's virtual condition – the smallest hole minus the max allowable perpendicularity error.
The hole on the right, the one that is not the datum, is called the ‘considered’ hole. In order to fit on the gage, the smallest considered hole must fit over the gage pin when the hole has position error equal to its positional tolerance.
The pin that the hole must fit over needs to be at its virtual condition – the smallest hole minus the positional tolerance value.
The hole on the left is the datum feature. The gage pin at the datum feature must be small enough for the smallest datum hole to fit over the pin when the datum hole has its maximum allowable perpendicularity error. Therefore the gage pin for the datum feature must be equal to the datum feature's virtual condition – the smallest hole minus the max allowable perpendicularity error.
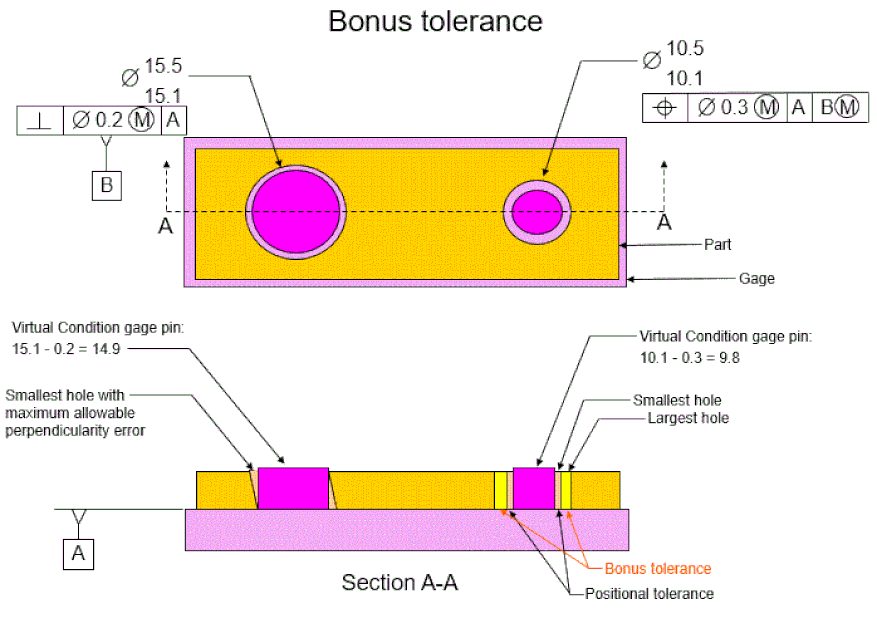
When the considered hole is at its largest, the hole can move an additional amount and still fit on the gage. This additional allowable movement is called Bonus Tolerance.
Let's re-visit the fence. Instead of planting a bunch of posts in the ground and hoping that we can get them perpendicular to the ground, we are going to switch to using some pre-manufactured fence sections. One of these sections is shown below. The company that makes these fence sections does such precise work that we will consider the dimensions to be perfect. We know that at a microscopic level there will be some error, but it will be so small that we will consider it to be perfect.
We tend to do the same thing with gages in industry. We know that they are not made perfect, but the error is so small that from our perspective as product designers we consider the gages to be perfect.
Our fence sections will have posts that are exactly 5 diameter and their center lines will be exactly 50 apart. And of course the posts are exactly parallel to each other.
We tend to do the same thing with gages in industry. We know that they are not made perfect, but the error is so small that from our perspective as product designers we consider the gages to be perfect.
Our fence sections will have posts that are exactly 5 diameter and their center lines will be exactly 50 apart. And of course the posts are exactly parallel to each other.
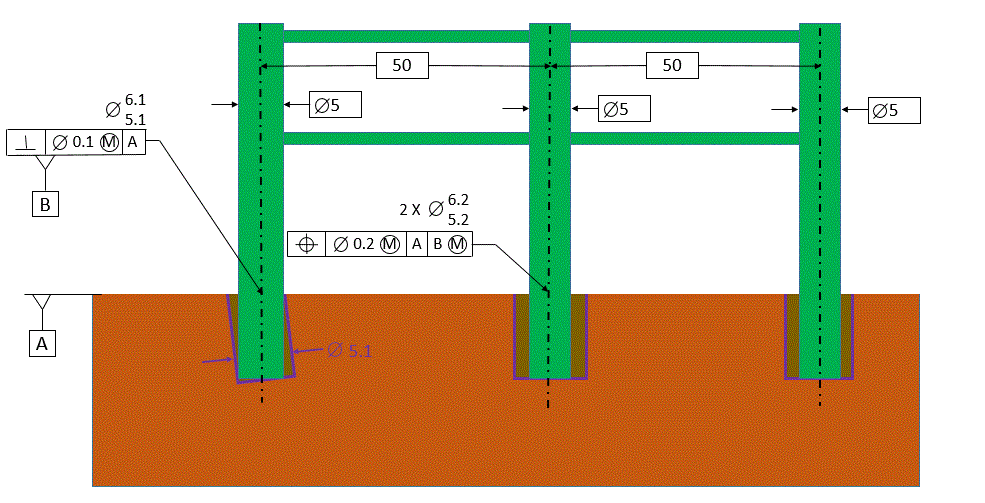
Now we just need to dig our holes and slide the fence section into our holes. Once again we will make the far left hole our datum and locate our other holes relative to our datum hole. Our datum hole has size tolerance and perpendicularity tolerance. Because we want to forget about the tolerances on our datum hole for now and focus on the other holes, we will consider our datum hole to be at its smallest allowable size and at its maximum allowable perpendicularity error. In this case, the hole will leave a space for the post that is equal to the virtual condition size of the hole. The virtual condition size is the smallest hole minus the perpendicularity error. So the virtual condition of our datum hole is 5.1-0.1=5.0. This is also the exact size of the post that goes in the datum hole. Therefore the post will fit snug in the hole and we will forget about it for now. We will re-visit our datum hole later, after we learn everything there is to know about the other two holes.
The holes that are not the datum hole are referred to as the "Considered holes" or the "Measured holes". That just means the holes that are not the datum hole.
Our considered holes will have both size tolerance and location tolerance. We want to make sure that the combination of size tolerance and location tolerance always protects a hole (or a boundary) such that the fence post will always fit in the hole. We do this by specifying our holes a basic 50 apart and with a virtual condition that is equal to the size of the fence post.
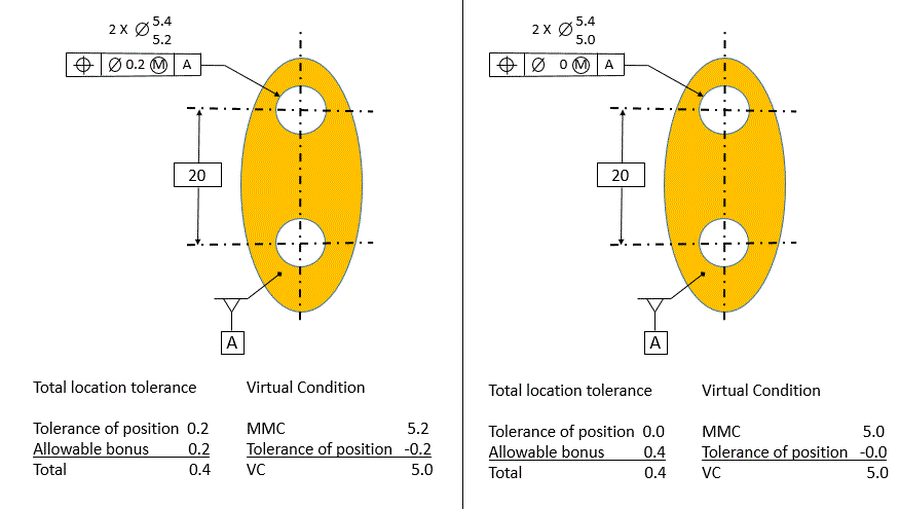
The size of the fence post, and therefore the boundary that we cannot violate, is 5 diameter. Therefore the smallest hole minus the location tolerance must equal 5.
The best we can do for locating our smallest hole is to hold it within a tolerance of position of 0.2. Therefore the smallest that our hole can be and always have the fence post go in is 5.0+0.2=5.2. We also know that the best we can do in controlling the size of our hole is to allow the diameter to vary by 1.0. Therefore the largest hole allowed will be 5.2+1.0=6.2.
Now we have our hole with a size of 5.2-6.2 and a tolerance of position of 0.2.
As long as our fence sections are the same, then the same tolerances will work on both holes. Therefore we can have a pattern of two holes with exactly the same location and size tolerance.
Note that in this case we have also included the Maximum Material Condition (MMC) modifier on our tolerance of position. That is because we know that the larger we make the hole, the more location error it can have and the fence post will still fit in it.
The holes that are not the datum hole are referred to as the "Considered holes" or the "Measured holes". That just means the holes that are not the datum hole.
Our considered holes will have both size tolerance and location tolerance. We want to make sure that the combination of size tolerance and location tolerance always protects a hole (or a boundary) such that the fence post will always fit in the hole. We do this by specifying our holes a basic 50 apart and with a virtual condition that is equal to the size of the fence post.
The size of the fence post, and therefore the boundary that we cannot violate, is 5 diameter. Therefore the smallest hole minus the location tolerance must equal 5.
The best we can do for locating our smallest hole is to hold it within a tolerance of position of 0.2. Therefore the smallest that our hole can be and always have the fence post go in is 5.0+0.2=5.2. We also know that the best we can do in controlling the size of our hole is to allow the diameter to vary by 1.0. Therefore the largest hole allowed will be 5.2+1.0=6.2.
Now we have our hole with a size of 5.2-6.2 and a tolerance of position of 0.2.
As long as our fence sections are the same, then the same tolerances will work on both holes. Therefore we can have a pattern of two holes with exactly the same location and size tolerance.
Note that in this case we have also included the Maximum Material Condition (MMC) modifier on our tolerance of position. That is because we know that the larger we make the hole, the more location error it can have and the fence post will still fit in it.
The animation below illustrates how using the MMC modifier assures that the posts will always fit in the holes.
First consider when the holes are perfectly perpendicular to datum [A]. When the hole is at its smallest allowable size (MMC) of 5.2 dia, the allowable location error is 0.2. We see in the animation that the centerline of the hole can be 0.1 away (radially) from the center of the post, and the post will still fit in the hole.
When the hole is at its largest size (LMC) of 6.2 dia, the allowable location error is the original 0.2 dia plus the size tolerance of 1.0 for a total location error allowed of 1.2. We see in the animation that the centerline of the hole can be 0.6 away (radially) from the center of the post, and the post will still fit in the hole.
The difference between the 0.2 location tolerance allowed when the hole is at its smallest allowable (MMC) size and the 1.2 location tolerance allowed when the hole is at its largest (LMC) size is called bonus tolerance. The purpose of bonus tolerance is to allow the hole to have more location error as the hole gets larger and still always have the post be able to fit in the hole. For any given hole, the bonus tolerance is equal to the actual size of the hole minus the smallest size of the hole. The maximum bonus tolerance allowed is when the hole is at its largest allowable size. Therefore the maximum bonus tolerance allowed is always equal to the size tolerance.
Now consider the case when the hole is centered but tilted. The tolerance of position limits the amount that the hole can tilt. When the hole is at its smallest (MMC) allowable size, the hole is allowed to tilt a little bit and the post can still fit in the hole. When the hole is at its largest (LMC) allowable size, the hole can tilt more and the post still fits in the hole.
Ultimately the size and location and tilting of the hole all work together to allow as much tolerance as possible but always protect a boundary so that the post will always fit in the hole.
First consider when the holes are perfectly perpendicular to datum [A]. When the hole is at its smallest allowable size (MMC) of 5.2 dia, the allowable location error is 0.2. We see in the animation that the centerline of the hole can be 0.1 away (radially) from the center of the post, and the post will still fit in the hole.
When the hole is at its largest size (LMC) of 6.2 dia, the allowable location error is the original 0.2 dia plus the size tolerance of 1.0 for a total location error allowed of 1.2. We see in the animation that the centerline of the hole can be 0.6 away (radially) from the center of the post, and the post will still fit in the hole.
The difference between the 0.2 location tolerance allowed when the hole is at its smallest allowable (MMC) size and the 1.2 location tolerance allowed when the hole is at its largest (LMC) size is called bonus tolerance. The purpose of bonus tolerance is to allow the hole to have more location error as the hole gets larger and still always have the post be able to fit in the hole. For any given hole, the bonus tolerance is equal to the actual size of the hole minus the smallest size of the hole. The maximum bonus tolerance allowed is when the hole is at its largest allowable size. Therefore the maximum bonus tolerance allowed is always equal to the size tolerance.
Now consider the case when the hole is centered but tilted. The tolerance of position limits the amount that the hole can tilt. When the hole is at its smallest (MMC) allowable size, the hole is allowed to tilt a little bit and the post can still fit in the hole. When the hole is at its largest (LMC) allowable size, the hole can tilt more and the post still fits in the hole.
Ultimately the size and location and tilting of the hole all work together to allow as much tolerance as possible but always protect a boundary so that the post will always fit in the hole.
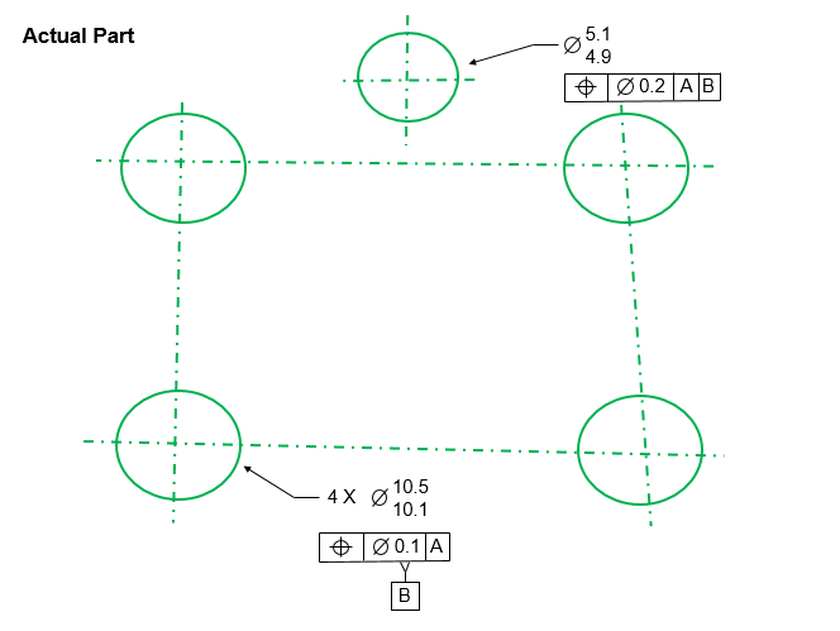
A hole has a size tolerance and a location tolerance. The actual size and location are measured. The question is whether or not the hole is in spec based on the measurements that were taken.
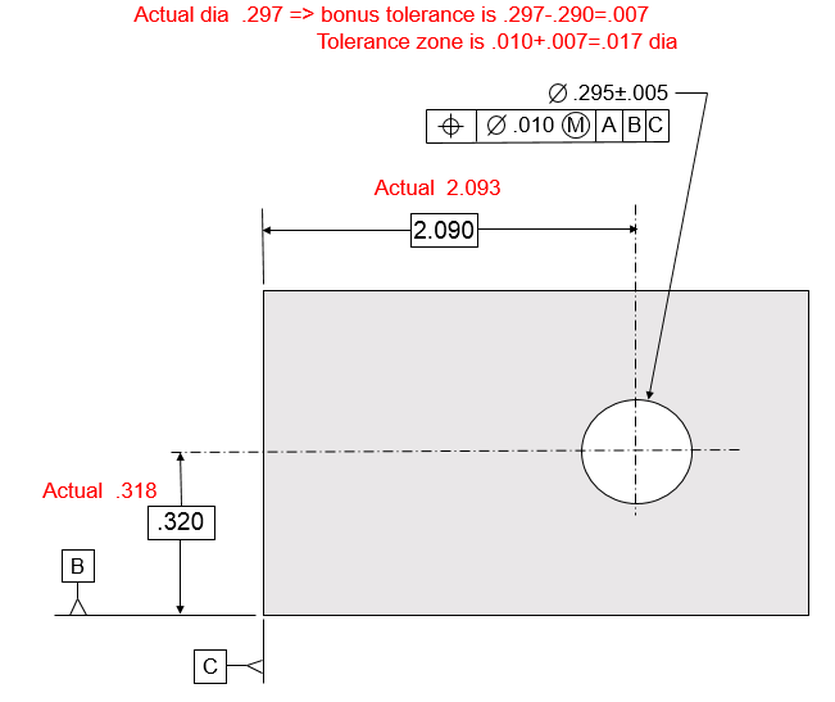
Below is the part with the hole, the specifications, and the actual size and locations as measured.
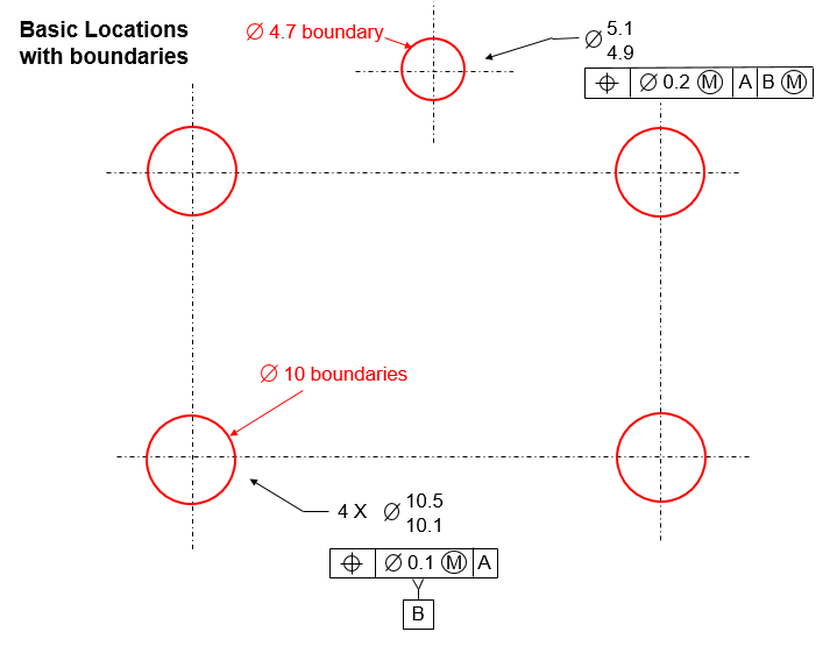
The location tolerance of .010 applies at the MMC hole size of .290
The actual size of the hole is .297, so there is a bonus tolerance of .007
The size of the tolerance zone for this hole is the original .010 plus the bonus tolerance of .007 for a total location tolerance zone of .017
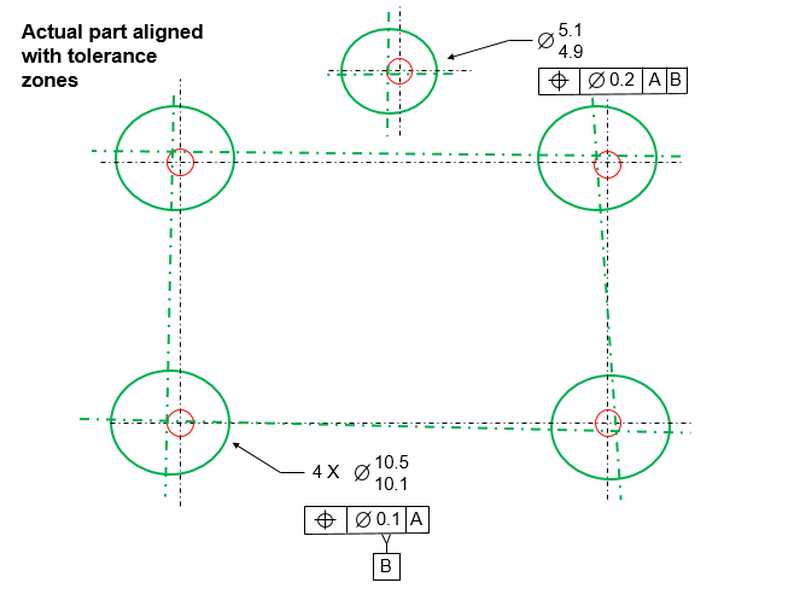
We also see that the actual location of the hole is off from its true position by .003 horizontally and .002 vertically.
Below is the part with the hole, the specifications, and the actual size and locations as measured.
The location tolerance of .010 applies at the MMC hole size of .290
The actual size of the hole is .297, so there is a bonus tolerance of .007
The size of the tolerance zone for this hole is the original .010 plus the bonus tolerance of .007 for a total location tolerance zone of .017
We also see that the actual location of the hole is off from its true position by .003 horizontally and .002 vertically.
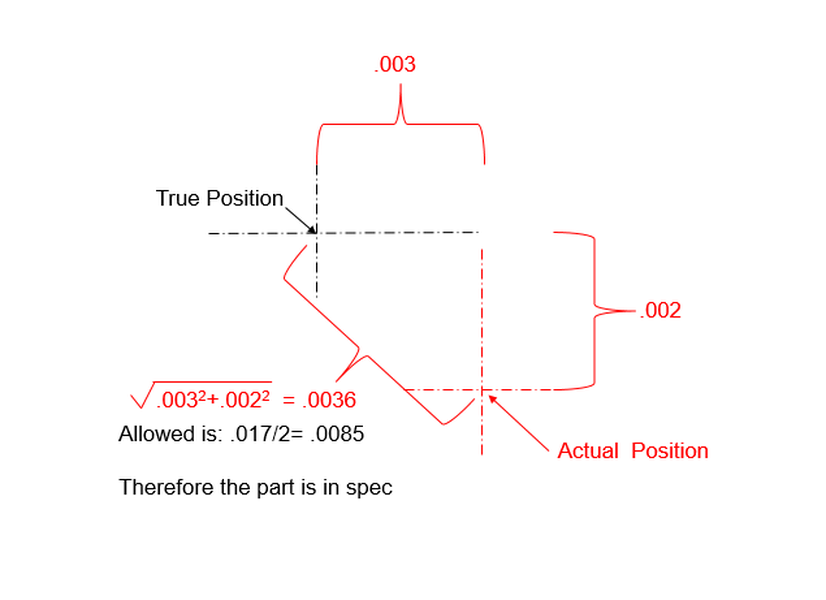
To calculate whether or not the hole meets the spec, we will look at the actual position of the hole relative to the true position of the hole. We see that they are offset by .003 horizontally and .002 vertically. We use the Pythagorean Theorem to calculate the radial distance of .0036
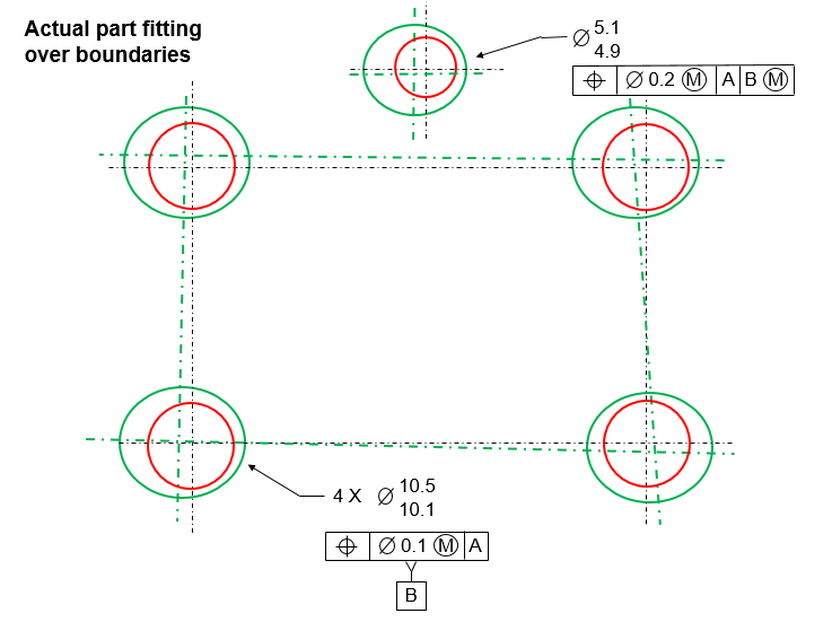
Now we recall that our location tolerance zone has a diameter of .017. This means that in any radial direction, our actual hole can be as much as .0085 away from its true position and still be in spec. Since our hole is only .0036 away from its true position and .0036 is less than .0085, we can conclude that the hole is within spec.
Now we recall that our location tolerance zone has a diameter of .017. This means that in any radial direction, our actual hole can be as much as .0085 away from its true position and still be in spec. Since our hole is only .0036 away from its true position and .0036 is less than .0085, we can conclude that the hole is within spec.
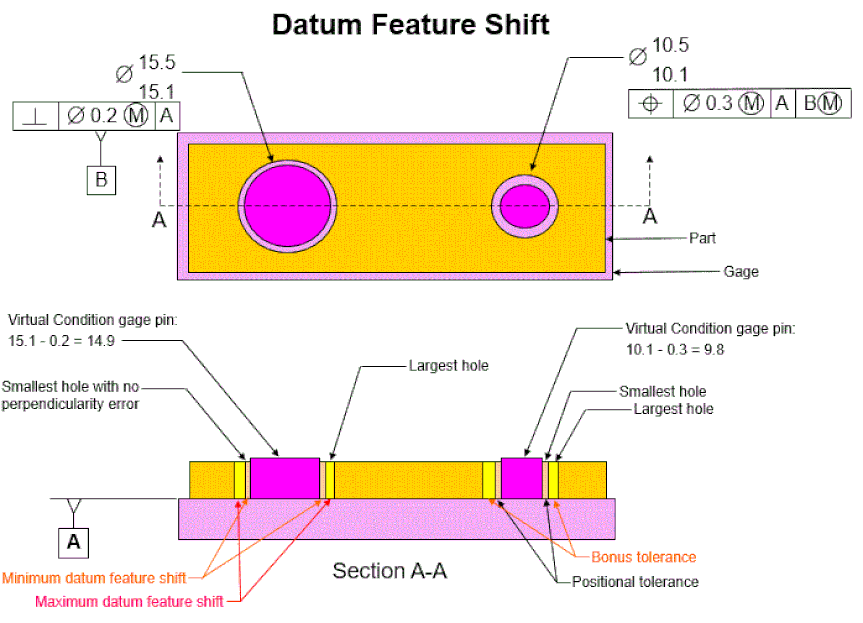
When the datum hole is at its smallest and does not have perpendicularity error, the datum hole can move an amount equal to the perpendicularity tolerance, and still fit on the gage. This allowable movement is called Minimum Datum Feature Shift.
Minimum Datum Feature Shift is equal to the smallest allowable datum hole size minus the virtual condition (MMB) size of the datum feature.
Minimum Datum Feature Shift is equal to the smallest allowable datum hole size minus the virtual condition (MMB) size of the datum feature.
When the datum hole is at its largest and does not have perpendicularity error, the datum hole can move an amount equal to the perpendicularity tolerance plus the size tolerance, and still fit on the gage. This allowable movement is called Maximum Datum Feature Shift.
Maximum Datum Feature Shift is equal to the largest allowable datum hole size minus the virtual condition (MMB) size of the datum feature.
Maximum Datum Feature Shift is equal to the largest allowable datum hole size minus the virtual condition (MMB) size of the datum feature.
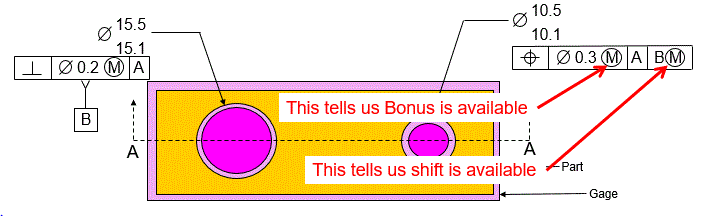
The modifiers in the Feature Control Frame, as shown above, tell us when we can have bonus and/or shift
Now we will examine the datum hole and introduce Datum Feature Shift.
The MMB symbol specifies that datum feature shift is allowed. The MMB symbol looks exactly like the MMC symbol. When it's in the tolerance portion of a feature control frame, it's MMC. When it's in the datum section of the feature control frame it's MMB.
In our discussion thus far, the datum hole has had the maximum amount of perpendicularity error allowed by the perpendicularity control.
The MMB symbol specifies that datum feature shift is allowed. The MMB symbol looks exactly like the MMC symbol. When it's in the tolerance portion of a feature control frame, it's MMC. When it's in the datum section of the feature control frame it's MMB.
In our discussion thus far, the datum hole has had the maximum amount of perpendicularity error allowed by the perpendicularity control.
When the datum hole is perfectly perpendicular to datum [A], there is looseness between the hole and the post. Remember that the post serves the same function as a gage. Always remember that datum feature shift is equal to the looseness between the hole and the gage. As long as you remember that, you will never need to memorize any formulas.
When the hole is at its smallest (MMC) size of 5.1, it is 0.1 larger than the post. So the datum feature shift is 0.1 from a diameter perspective. Therefore the hole can be 0.05 closer to the considered holes or 0.05 farther away from the considered holes and in either case the post (the gage) will still fit in the datum hole while the other posts still fit in the considered holes.
When the hole is at its smallest (MMC) size of 5.1, it is 0.1 larger than the post. So the datum feature shift is 0.1 from a diameter perspective. Therefore the hole can be 0.05 closer to the considered holes or 0.05 farther away from the considered holes and in either case the post (the gage) will still fit in the datum hole while the other posts still fit in the considered holes.
When the hole is at its largest (LMC) allowable size of 6.1, then the hole is 1.1 larger than the post (the gage). Therefore the allowable datum feature shift is 1.1 on a diameter basis. So the hole can shift 0.55 closer to the considered holes or 0.55 farther away from the considered holes and the posts will still fit in the holes.
So the size and the location work together to allow as much location error as possible while always enabling the posts to fit in the holes.
So the size and the location work together to allow as much location error as possible while always enabling the posts to fit in the holes.
Now we will take a closer look at the fence section itself. We said before that the fence section is so well made that we will consider it to be perfect even though we know that it is not really perfect. So now we will apply some tolerances to it.
We see the fence section below fitting into a gage that has been created to make sure that the fence section does not violate its spec limits. The gage is a fixed size gage - the hole sizes in the gage do not change. We can use a fixed size gage when our features of size are called out MMC and MMB. The feature control frame for the considered posts calls out the 0.1 dia tolerance at MMC, and it references datum [A] at MMB.
Also note that the post on the left is the primary datum, not secondary. The posts are not held perpendicular to some surface. The post on the left is the datum, and the other two posts are both located and oriented relative to the primary datum. The tolerance of position is controlling location and parallelism.
If the considered posts are located perfectly, they could have parallelism error of 0.1. This would be distributed over the entire height of the post, so we would probably not be able to visually see it.
We will assume that the posts are perfectly parallel to each other, and we will focus on the location error allowed by the tolerance of position.
We see the fence section below fitting into a gage that has been created to make sure that the fence section does not violate its spec limits. The gage is a fixed size gage - the hole sizes in the gage do not change. We can use a fixed size gage when our features of size are called out MMC and MMB. The feature control frame for the considered posts calls out the 0.1 dia tolerance at MMC, and it references datum [A] at MMB.
Also note that the post on the left is the primary datum, not secondary. The posts are not held perpendicular to some surface. The post on the left is the datum, and the other two posts are both located and oriented relative to the primary datum. The tolerance of position is controlling location and parallelism.
If the considered posts are located perfectly, they could have parallelism error of 0.1. This would be distributed over the entire height of the post, so we would probably not be able to visually see it.
We will assume that the posts are perfectly parallel to each other, and we will focus on the location error allowed by the tolerance of position.
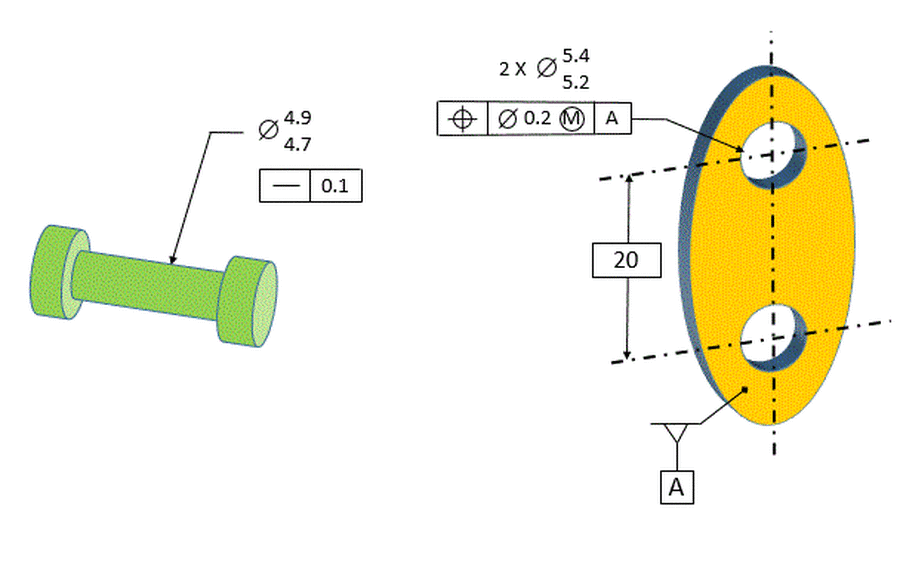
When the considered posts are at their largest (MMC) size of 4.9, 0.1 dia of location error is allowed. Therefore the posts can be 0.05 radially closer to or farther away from the datum post and still fit in the gage.
When the considered posts are at their smallest (LMC) size of 4.7, they can be radially 0.15 closer or farther away from the datum post and still fit in the gage. Therefore the max location error allowed for the considered posts at LMC is 0.3 dia. The 0.3 consists of the original 0.1 plus the 0.2 size tolerance. The additional 0.2 location tolerance that we get from the size tolerance is called the bonus tolerance.
When the considered posts are at their smallest (LMC) size of 4.7, they can be radially 0.15 closer or farther away from the datum post and still fit in the gage. Therefore the max location error allowed for the considered posts at LMC is 0.3 dia. The 0.3 consists of the original 0.1 plus the 0.2 size tolerance. The additional 0.2 location tolerance that we get from the size tolerance is called the bonus tolerance.
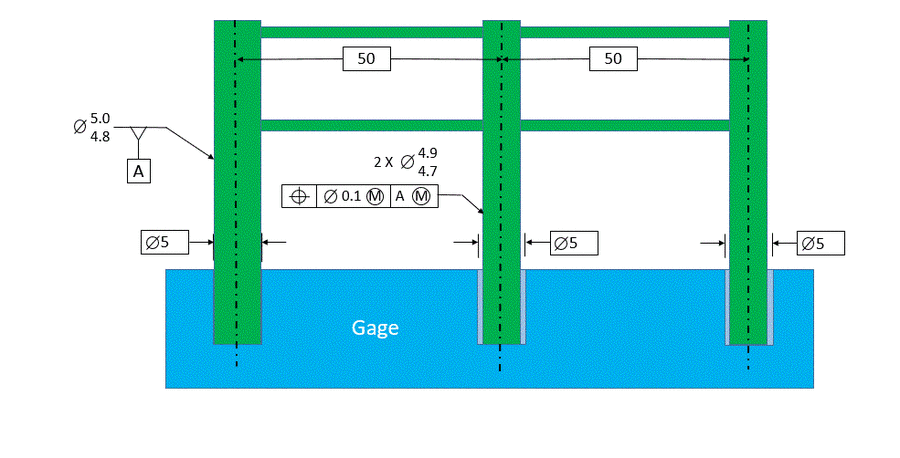
Now we will focus on the datum post. When the datum post is at its MMC size of 5.0, it fits snug into the gage. In fact, it may be necessary to tap it in with a rubber mallet. The datum post cannot shift at all relative to the considered posts.
When the datum post is at its LMC size of 4.8, it can be 0.1 closer to the considered posts or 0.1 farther away from the considered posts and still fit in the gage. So it can shift 0.2 on a diameter basis. This 0.2 dia maximum that the feature can shift relative to the considered posts when the datum post is at its LMC size is called datum feature shift. If the post were manufactured somewhere between 4.8 dia and 5.0 dia, then the allowable datum feature shift would be a value between zero and 0.2. Once again, always remember that the amount of datum feature shift allowed is equal to the looseness between the datum feature and the gage.
Now we have specified fence posts that will always fit into boundaries that are exactly 5.0 dia and exactly 50 apart. In the previous section we specified post holes that will never violate boundaries that are exactly 5.0 dia and exactly 50 apart. Therefore we now know that our fence posts will always fit into our post holes.
When the datum post is at its LMC size of 4.8, it can be 0.1 closer to the considered posts or 0.1 farther away from the considered posts and still fit in the gage. So it can shift 0.2 on a diameter basis. This 0.2 dia maximum that the feature can shift relative to the considered posts when the datum post is at its LMC size is called datum feature shift. If the post were manufactured somewhere between 4.8 dia and 5.0 dia, then the allowable datum feature shift would be a value between zero and 0.2. Once again, always remember that the amount of datum feature shift allowed is equal to the looseness between the datum feature and the gage.
Now we have specified fence posts that will always fit into boundaries that are exactly 5.0 dia and exactly 50 apart. In the previous section we specified post holes that will never violate boundaries that are exactly 5.0 dia and exactly 50 apart. Therefore we now know that our fence posts will always fit into our post holes.
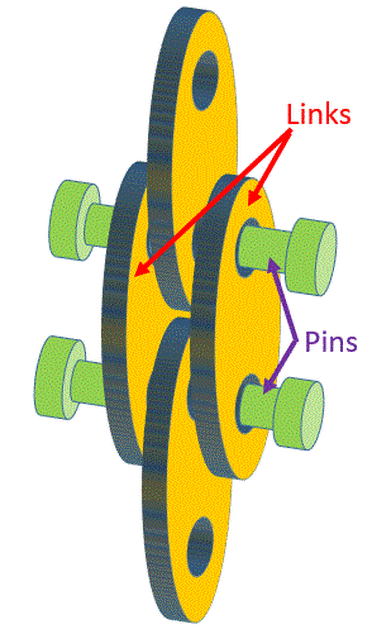
Our fence will use links that are held together by pins. The arrangement will be as shown to the right.
In order for the assembly to work, the holes in the links will need to be located accurately enough so that the pins will be able to go through the holes in the front link and the holes in the back link.
The pins represent boundaries that the holes may not violate. As long as the holes do not violate the boundaries represented by the pins, then the pins will go through the holes. If the holes do violate the boundaries represented by the pins, then the pins will not go through the holes and the links will not assemble.
In order for the assembly to work, the holes in the links will need to be located accurately enough so that the pins will be able to go through the holes in the front link and the holes in the back link.
The pins represent boundaries that the holes may not violate. As long as the holes do not violate the boundaries represented by the pins, then the pins will go through the holes. If the holes do violate the boundaries represented by the pins, then the pins will not go through the holes and the links will not assemble.
The figure below shows how we will dimension our pins and holes such that we know how much space the pins will require and we specify the holes such that they will always allow the pins to pass through the holes.
The pin is dimensioned with a size tolerance and a straightness applied to the feature of size. The pin will never take up a space greater than a perfect cylinder whose diameter is equal to the virtual condition (VC) of the pin. The virtual condition size of the pin is the MMC size of 4.9 plus the straightness tolerance of 0.1 which results in a VC size of 5.0.
The holes in the link have a tolerance of position of 0.2 dia at MMC. Therefore the holes will never be allowed to violate boundaries that are perfect cylinders, exactly perpendicular to datum [A], and the VC size of the holes. The VC size of the holes is the MMC size of 5.2 minus the tolerance of position of 0.2 for a VC size of 5.0.
The pins will always fit though a perfect cylinder of 5.0 dia, and the holes will always protect perfect cylinders, perpendicular to datum [A] and 5.0 dia. Therefore the pins will always go through the holes as long as the parts are within spec. Admittedly if we want to push a 5.0 pin through a 5.0 hole, we might have to push kind of hard. But we will assume no friction so that we theoretically will not have a problem. In reality, the chances are pretty small that we will encounter a pin that takes up a 5.0 dia cylinder at the same time that we encounter a hole that preserves no more than a 5.0 diameter boundary.
The pin is dimensioned with a size tolerance and a straightness applied to the feature of size. The pin will never take up a space greater than a perfect cylinder whose diameter is equal to the virtual condition (VC) of the pin. The virtual condition size of the pin is the MMC size of 4.9 plus the straightness tolerance of 0.1 which results in a VC size of 5.0.
The holes in the link have a tolerance of position of 0.2 dia at MMC. Therefore the holes will never be allowed to violate boundaries that are perfect cylinders, exactly perpendicular to datum [A], and the VC size of the holes. The VC size of the holes is the MMC size of 5.2 minus the tolerance of position of 0.2 for a VC size of 5.0.
The pins will always fit though a perfect cylinder of 5.0 dia, and the holes will always protect perfect cylinders, perpendicular to datum [A] and 5.0 dia. Therefore the pins will always go through the holes as long as the parts are within spec. Admittedly if we want to push a 5.0 pin through a 5.0 hole, we might have to push kind of hard. But we will assume no friction so that we theoretically will not have a problem. In reality, the chances are pretty small that we will encounter a pin that takes up a 5.0 dia cylinder at the same time that we encounter a hole that preserves no more than a 5.0 diameter boundary.
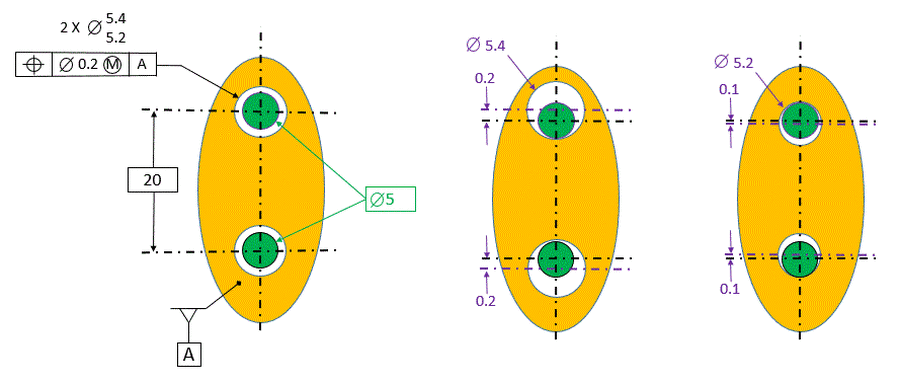
In the figure below we see the extremes of the hole sizes allowed and how they preserve a perfect 5 dia boundary for the pins. If the holes are at their LMC size of 5.4, the total location error allowed is 0.2 plus the 0.2 bonus tolerance for a total of 0.4 dia of location tolerance. Therefore the center of the hole can be 0.2 away from its basic location and without violating the green boundary.
When the holes are at their MMC size of 5.2, the total location error allowed is only 0.2. Therefore the center of the hole can be 0.1 away from its basic location without violating the green boundary.
When the holes are at their MMC size of 5.2, the total location error allowed is only 0.2. Therefore the center of the hole can be 0.1 away from its basic location without violating the green boundary.
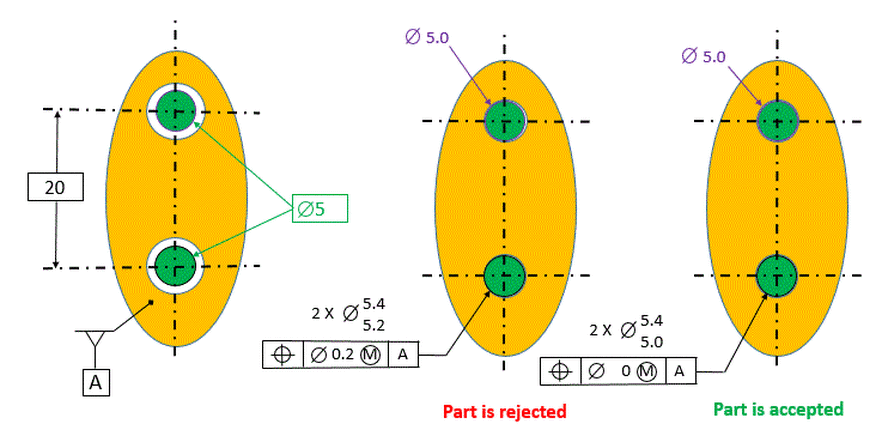
In the next figure, we see the hole at 5.0 dia. The part on the left is dimensioned the same way as it is in the figure above. The holes are located at exactly their perfect locations. So even though they are only 5.0 diameter, they do not violate the green boundary. The part would allow the pins to go through and function perfectly. But we must reject the part because the hole is smaller than its allowable MMC size.
The part on the right is dimensioned with zero positional tolerance at MMC. The tolerance of position is zero, and the MMC size specified in the size tolerance is 5.0 instead of 5.2. It's exactly the same as the part on the left - it will function perfectly. The only difference is that it is dimensioned in such a way that it is considered to be a good part.
The part on the right is dimensioned with zero positional tolerance at MMC. The tolerance of position is zero, and the MMC size specified in the size tolerance is 5.0 instead of 5.2. It's exactly the same as the part on the left - it will function perfectly. The only difference is that it is dimensioned in such a way that it is considered to be a good part.
The purpose of zero tolerancing at MMC is to allow functional parts to be accepted when they would be rejected by the more traditional method of tolerancing. The figure below shows a comparison of traditional tolerancing vs. zero tolerancing at MMC.
When our purpose is assembly, we are concerned about two things: How much location tolerance we are allowed, and what is the virtual condition of the holes - the boundary that will be protected in order to allow assembly of the mating part.
The total amount of location tolerance is the same with both methods. With the traditional method, the total location tolerance allowed is the O.2 allowed at MMC plus the bonus of 0.2 that we get from the size tolerance to make a total of 0.4. When the part has zero tolerance at MMC, the total location tolerance is the zero that we get at MMC plus the 0.4 bonus that we get from the size tolerance for a total of 0.4.
The virtual condition is also the same for both methods. For the traditional method, the virtual condition is the MMC size of 5.2 minus the location tolerance of 0.2 for a VC of 5.0. For the zero tolerance at MMC method, the virtual condition is the MMC size of 5.0 minus zero for a VC of 5.0.
Functionally, there is no down side to zero location tolerance at MMC. However, there may not be an up side either. If you make your holes with twist drills, you will never get an under sized hole. So the extra parts you get to keep because you did zero tolerancing at MMC will never actually exist. Also, zero tolerancing at MMC might cause confusion as to what nominal should be if manufacturing chooses to do a capability study.
When our purpose is assembly, we are concerned about two things: How much location tolerance we are allowed, and what is the virtual condition of the holes - the boundary that will be protected in order to allow assembly of the mating part.
The total amount of location tolerance is the same with both methods. With the traditional method, the total location tolerance allowed is the O.2 allowed at MMC plus the bonus of 0.2 that we get from the size tolerance to make a total of 0.4. When the part has zero tolerance at MMC, the total location tolerance is the zero that we get at MMC plus the 0.4 bonus that we get from the size tolerance for a total of 0.4.
The virtual condition is also the same for both methods. For the traditional method, the virtual condition is the MMC size of 5.2 minus the location tolerance of 0.2 for a VC of 5.0. For the zero tolerance at MMC method, the virtual condition is the MMC size of 5.0 minus zero for a VC of 5.0.
Functionally, there is no down side to zero location tolerance at MMC. However, there may not be an up side either. If you make your holes with twist drills, you will never get an under sized hole. So the extra parts you get to keep because you did zero tolerancing at MMC will never actually exist. Also, zero tolerancing at MMC might cause confusion as to what nominal should be if manufacturing chooses to do a capability study.
Now we will use the Least Material Condition (LMC) modifier and the Least Material Boundary (LMB) modifier to solve a breeding problem.
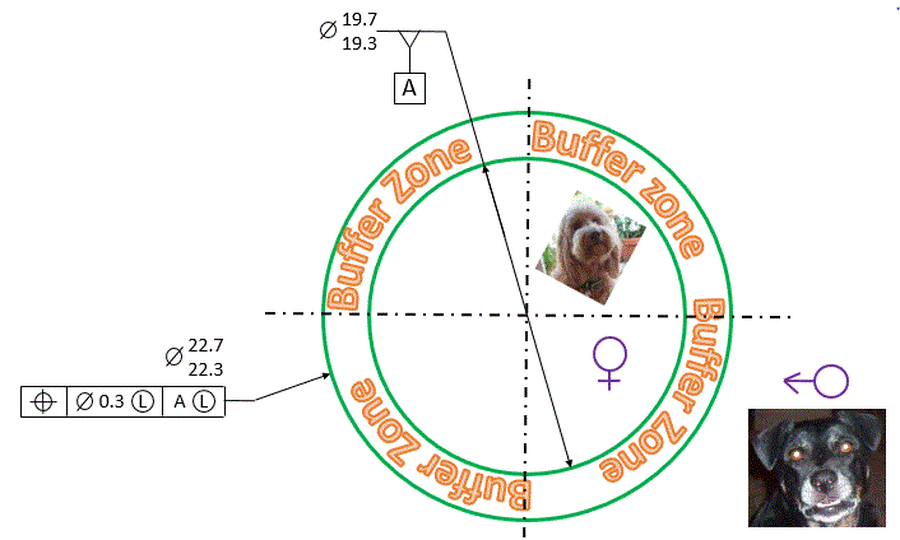
We have a male dog and a female dog who have not been neutered. At this point we do not want puppies, so when the female dog is in heat we need to keep the two dogs apart. If we just use a single chain link fence, the dogs might get creative and still manage to get pregnant. So we will use two fences and maintain a buffer zone in between.
Each of the circular fences has a size tolerance, and we need to locate the outer fence relative to the inner fence. Datum [A] is the axis of the unrelated actual mating envelope of the inner fence. There is an assumed basic zero dimension between Datum [A] and the axis of the unrelated actual mating envelope of the outer fence.
We want to make sure that the buffer zone never gets thinner than 1.15 feet. We specify the LMC modifier and the LMB modifier in the feature control frame in order to help us maintain this minimum distance.
We have a male dog and a female dog who have not been neutered. At this point we do not want puppies, so when the female dog is in heat we need to keep the two dogs apart. If we just use a single chain link fence, the dogs might get creative and still manage to get pregnant. So we will use two fences and maintain a buffer zone in between.
Each of the circular fences has a size tolerance, and we need to locate the outer fence relative to the inner fence. Datum [A] is the axis of the unrelated actual mating envelope of the inner fence. There is an assumed basic zero dimension between Datum [A] and the axis of the unrelated actual mating envelope of the outer fence.
We want to make sure that the buffer zone never gets thinner than 1.15 feet. We specify the LMC modifier and the LMB modifier in the feature control frame in order to help us maintain this minimum distance.
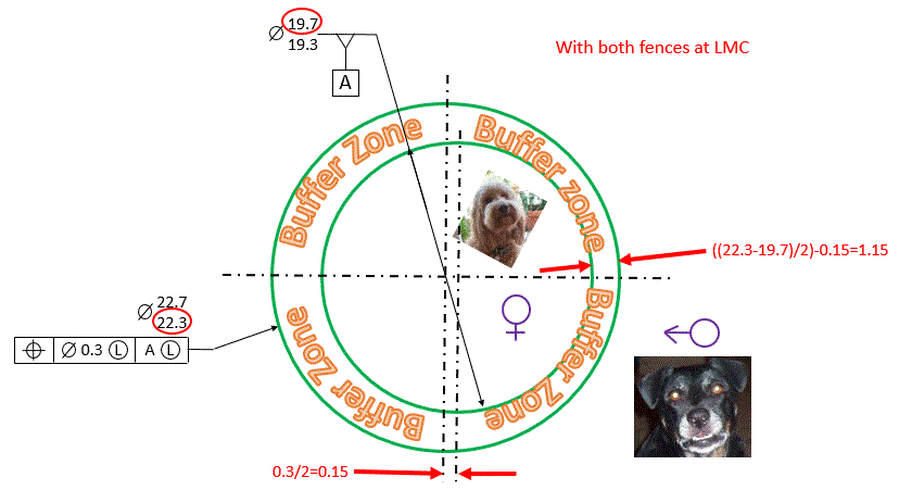
When the inner and outer fences are both at their LMC sizes, the tolerance of position of 0.3 dia applies. Therefore the center of the outer fence is allowed to be 0.15 radially away from the center of the inner fence. The minimum distance between the fences then is the difference between their radii minus the offset of the centers. As shown below this results in a value of 1.15.
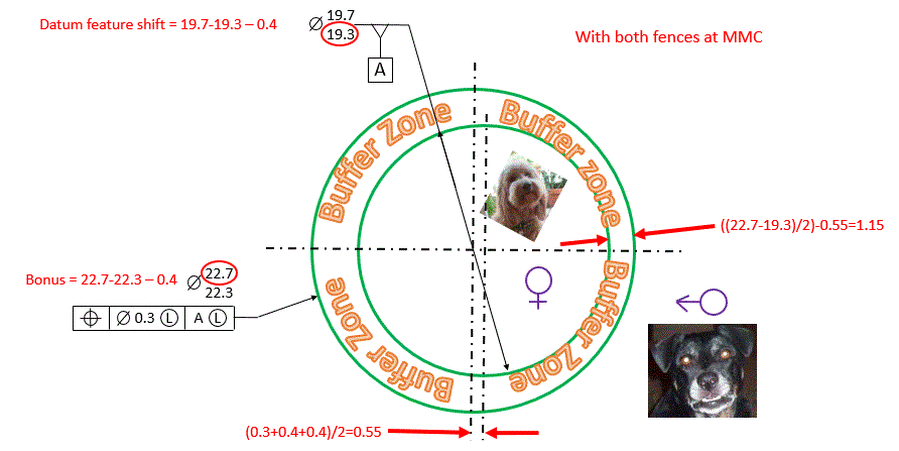
When the inner and outer fences are at their MMC sizes, the maximum bonus tolerance and the maximum datum feature shift are allowed. The maximum bonus tolerance is equal to the size tolerance of the outer fence. This is 0.4 dia or 0.2 radially.
The maximum datum feature shift is, as always, equal to the looseness between the part and the gage. Remember that with the LMC and LMB modifiers, the boundary that is being protected is inside the material. Therefore the gage is inside the material. In this case, the gage is in the buffer zone. So the gage for datum [A] is at the LMC size of 19.7. The max looseness between the part and the gage occurs when the part is at its MMC size of 19.3 Therefore the max datum feature shift allowed is 19.7-19.3=0.4 dia. The max datum feature shift allowed then is 0.2 radially.
The maximum that the center of the outer fence can be from the center of the inner fence is then the original 0.15 allowed by the 0.3 dia tolerance plus the 0.2 radial bonus tolerance plus the 0.2 radial datum shift for a total of 0.55.
The minimum that the two fences can be apart is equal to the difference in their radii minus the allowable offset of the centers. This adds up to 1.15.
The maximum datum feature shift is, as always, equal to the looseness between the part and the gage. Remember that with the LMC and LMB modifiers, the boundary that is being protected is inside the material. Therefore the gage is inside the material. In this case, the gage is in the buffer zone. So the gage for datum [A] is at the LMC size of 19.7. The max looseness between the part and the gage occurs when the part is at its MMC size of 19.3 Therefore the max datum feature shift allowed is 19.7-19.3=0.4 dia. The max datum feature shift allowed then is 0.2 radially.
The maximum that the center of the outer fence can be from the center of the inner fence is then the original 0.15 allowed by the 0.3 dia tolerance plus the 0.2 radial bonus tolerance plus the 0.2 radial datum shift for a total of 0.55.
The minimum that the two fences can be apart is equal to the difference in their radii minus the allowable offset of the centers. This adds up to 1.15.
We have seen now that the minimum distance allowed between the two fences is 1.15 when the fences are at their LMC and LMB sizes, and it is also 1.15 when the two fences are at their MMC and MMB sizes. This is what the LMC and LMB modifier do for us. They preserve a minimum distance such as a minimum wall thickness.
Now let's contrast what the various datums and tolerance zones are based on different ways of calling out datum references in feature control frames.
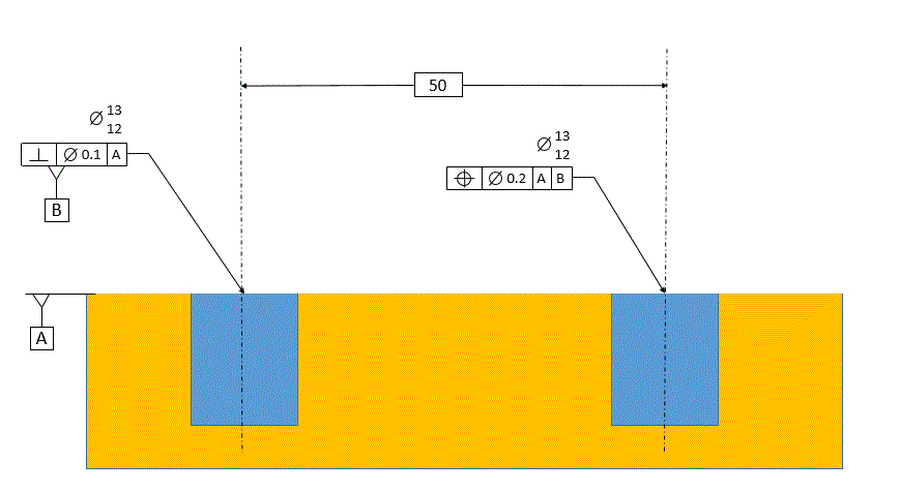
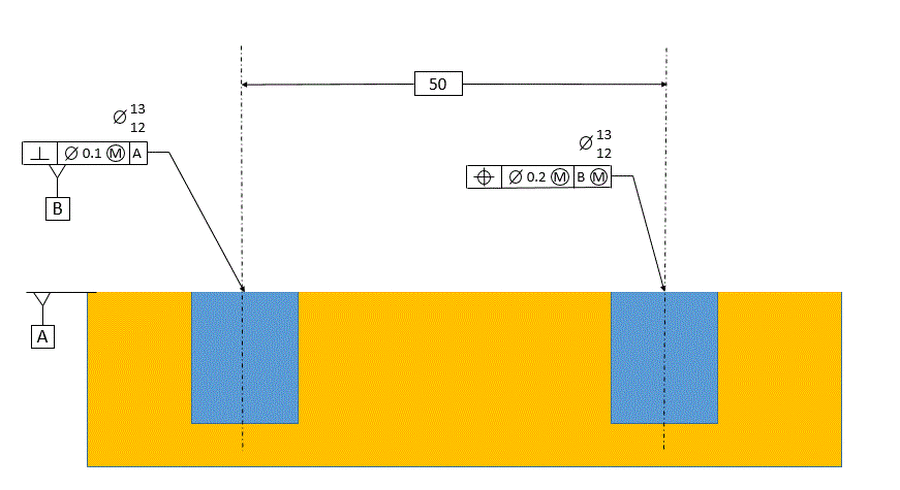
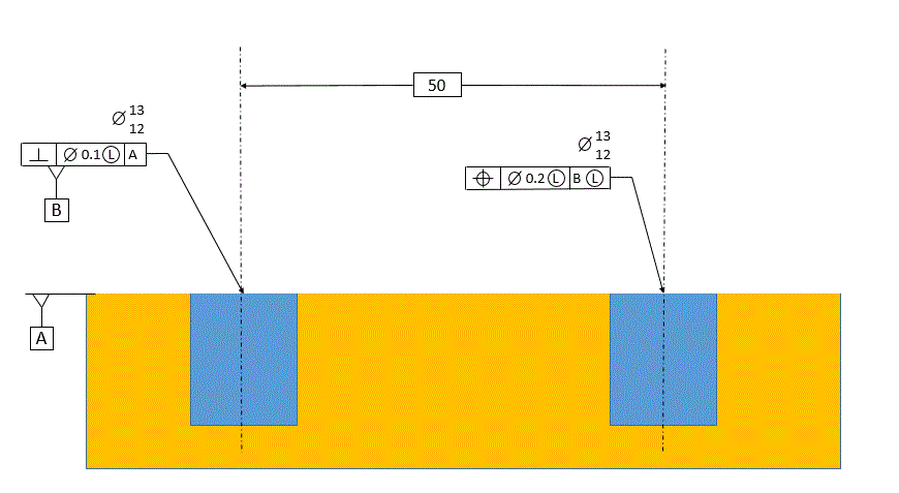
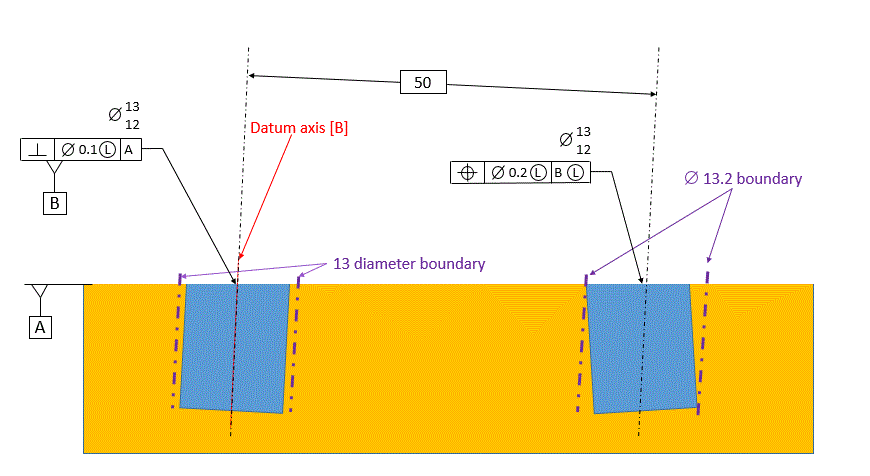
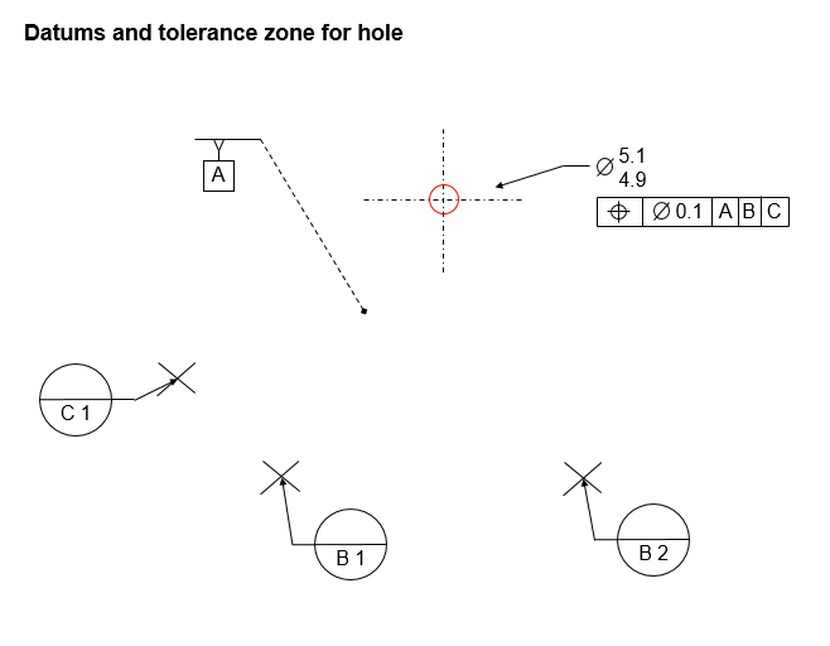
We will start with the simplest case below. Datum feature [B] has a perpendicularity control to datum plane [A], and the considered hole has a tolerance of position at RFS relative to datum [B] at RMB.
Since our considered hole is called out relative to datum [B] primary, we do not consider datum [A] in any way when establishing our datum. Datum [B] is the axis of the unrelated actual mating envelope of datum feature [B].
Our tolerance zone, for the considered hole, is a 0.2 dia tolerance zone that is exactly parallel to datum [B]. Once again, there is no relationship between the tolerance zone and datum [A].
The requirement for the tolerance of position callout is that the axis of the unrelated actual mating envelope of the considered hole must fall within the 0.2 dia tolerance zone.
Our tolerance zone, for the considered hole, is a 0.2 dia tolerance zone that is exactly parallel to datum [B]. Once again, there is no relationship between the tolerance zone and datum [A].
The requirement for the tolerance of position callout is that the axis of the unrelated actual mating envelope of the considered hole must fall within the 0.2 dia tolerance zone.
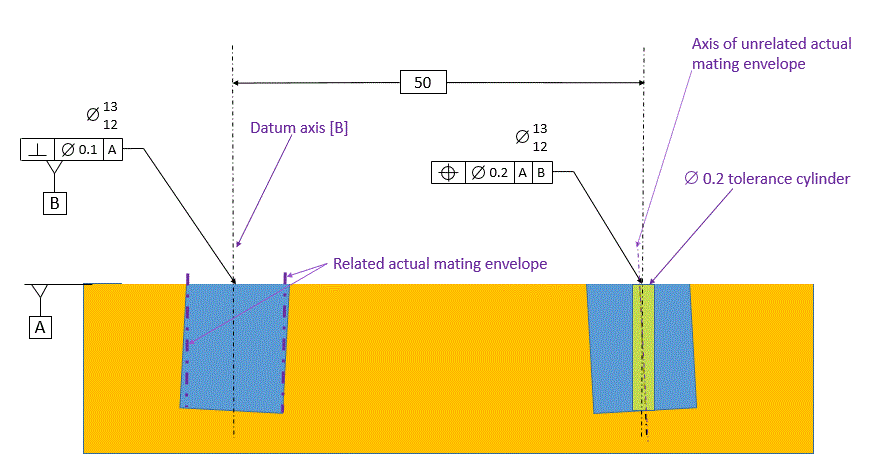
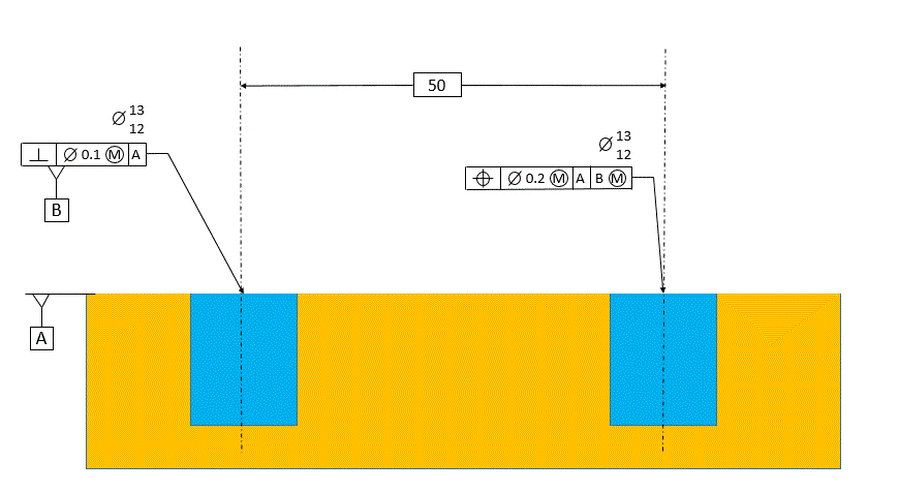
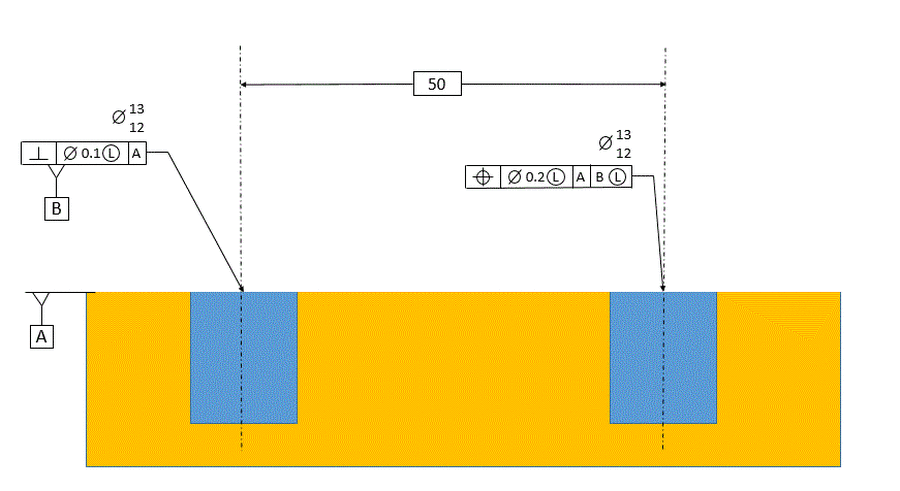
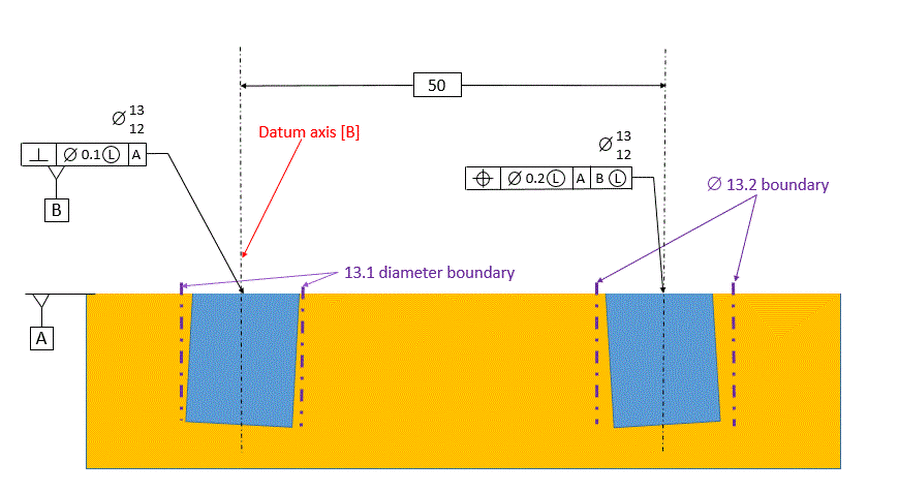
In the figure below, the tolerance of position references datum [A] primary and datum [B] secondary.
Now datum [B] is defined as being exactly perpendicular to datum [A]. It is the axis of the related actual mating envelope of the datum feature. The tolerance zone for the considered feature now is also perpendicular to datum [A] as well as parallel to datum [B]. The axis of the unrelated actual mating envelope of the considered hole must fall within the tolerance zone.
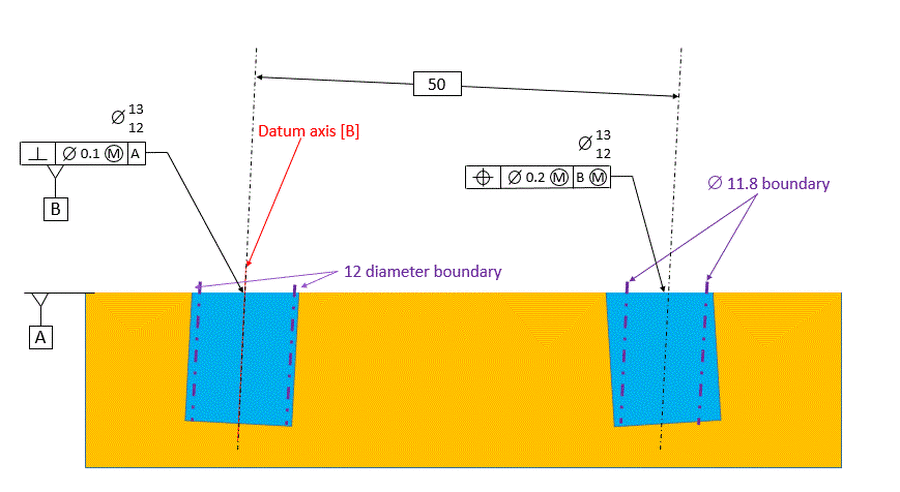
Next we will bring in the MMC and MMB modifiers. Once again the considered hole is located relative to [B] primary. Since we are specifying features of size at MMC and MMB, we will be looking at fixed size boundaries.
Datum [B] is the axis of a fixed size boundary. Since the considered feature calls out datum [B] as primary, we do not consider any relationship between datum [B] and datum [A]. Therefore datum [B] is the axis of a 12 diameter boundary. The 12 diameter boundary is inside the datum feature but not necessarily perpendicular to datum [A].
Our considered hole must not violate a fixed size boundary that is the virtual condition size of the hole - 11.8 diameter. This 11.8 diameter boundary is exactly parallel to the 12 diameter boundary from the datum feature. Neither boundary is perpendicular to datum [A].
Our considered hole must not violate a fixed size boundary that is the virtual condition size of the hole - 11.8 diameter. This 11.8 diameter boundary is exactly parallel to the 12 diameter boundary from the datum feature. Neither boundary is perpendicular to datum [A].
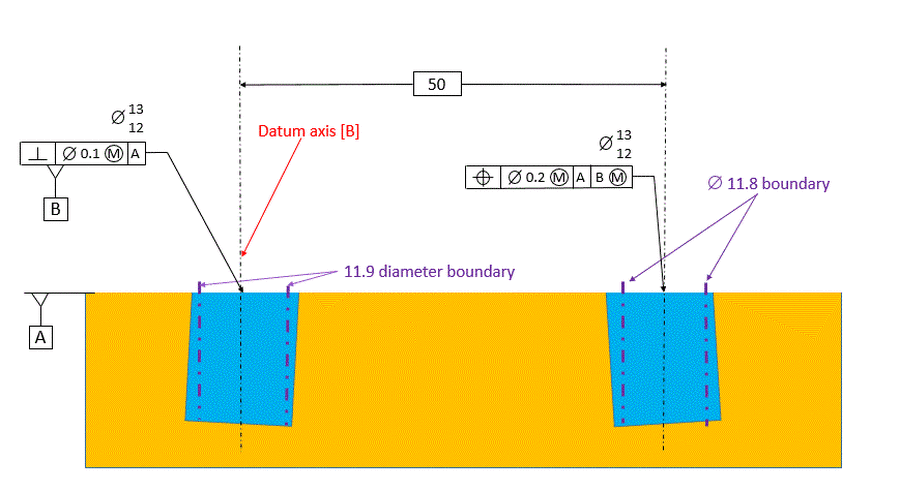
Next we consider the case in which our considered hole is called out MMC relative to datum [A] primary and datum [B] secondary at MMB.
Since the considered feature references [A] primary, our boundaries are now by definition exactly perpendicular to datum [A]. Datum [B] is the axis of the 11.9 boundary that is inside datum feature [B] and perpendicular to datum [A]. The boundary is 11.9 because that is the virtual condition size of the datum feature now that we consider perpendicularity relative to datum [A].
The tolerance zone that our considered hole must not violate is an 11.8 dia boundary that is exactly parallel to datum [B] and exactly perpendicular to datum [A].
The tolerance zone that our considered hole must not violate is an 11.8 dia boundary that is exactly parallel to datum [B] and exactly perpendicular to datum [A].
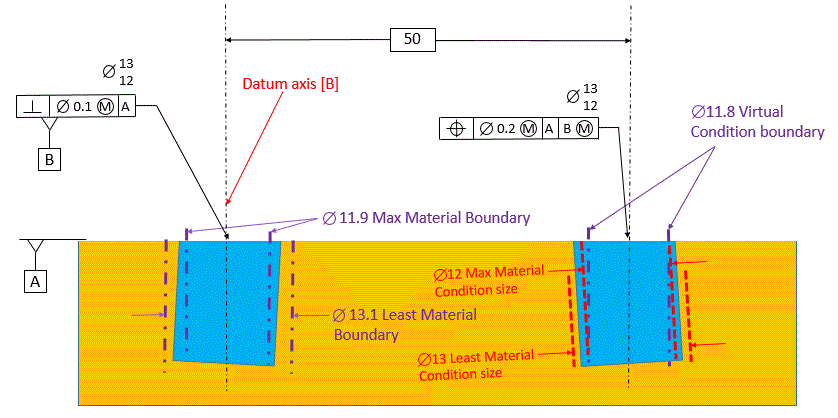
Now we will look at our considered hole called out LMC with the datum called out LMB.
Once again since our considered feature references datum [B] primary and datum [A] is not referenced, datum [A] will not be considered when determining our boundaries.
Datum [B] is the axis of a fixed size boundary that is inside the material. Since any relationship to datum [A] is not considered, the size of the boundary is 13. The Boundary is not perpendicular to datum [A]. In this case, instead of the fixed boundary being inside the datum feature, the datum feature is inside the fixed boundary.
The tolerance zone for the considered hole is a boundary that is the virtual condition size of the considered hole. Since we are specifying LMC, the virtual condition size of the considered hole is 13.2. The boundary is inside the material. Instead of the boundary being inside the considered hole, the considered hole is inside the boundary. The boundary for the considered hole is exactly parallel to datum [B] and is not perpendicular to datum [A].
Datum [B] is the axis of a fixed size boundary that is inside the material. Since any relationship to datum [A] is not considered, the size of the boundary is 13. The Boundary is not perpendicular to datum [A]. In this case, instead of the fixed boundary being inside the datum feature, the datum feature is inside the fixed boundary.
The tolerance zone for the considered hole is a boundary that is the virtual condition size of the considered hole. Since we are specifying LMC, the virtual condition size of the considered hole is 13.2. The boundary is inside the material. Instead of the boundary being inside the considered hole, the considered hole is inside the boundary. The boundary for the considered hole is exactly parallel to datum [B] and is not perpendicular to datum [A].
Now we will look at our considered hole called out LMC relative to datum [A] primary and datum [B] secondary at LMB.
Since datum [A] is referenced primary, our boundaries will be exactly perpendicular to datum [A].
Datum [B] is the axis of the 13.1 diameter boundary that is exactly perpendicular to datum [A]. Datum feature [B] must be inside this boundary.
The boundary that the considered hole must not violate is the 13.2 diameter boundary that is exactly parallel to datum [B] and exactly perpendicular to datum [A]. This boundary is inside the material, and the considered hole must fit within this boundary.
Datum [B] is the axis of the 13.1 diameter boundary that is exactly perpendicular to datum [A]. Datum feature [B] must be inside this boundary.
The boundary that the considered hole must not violate is the 13.2 diameter boundary that is exactly parallel to datum [B] and exactly perpendicular to datum [A]. This boundary is inside the material, and the considered hole must fit within this boundary.
The following figures illustrate how Tolerance Of Position controls the perpendicularity of a hole or a pin. The same principles apply if the Tolerance Of Position is controlling a slot or a tab.
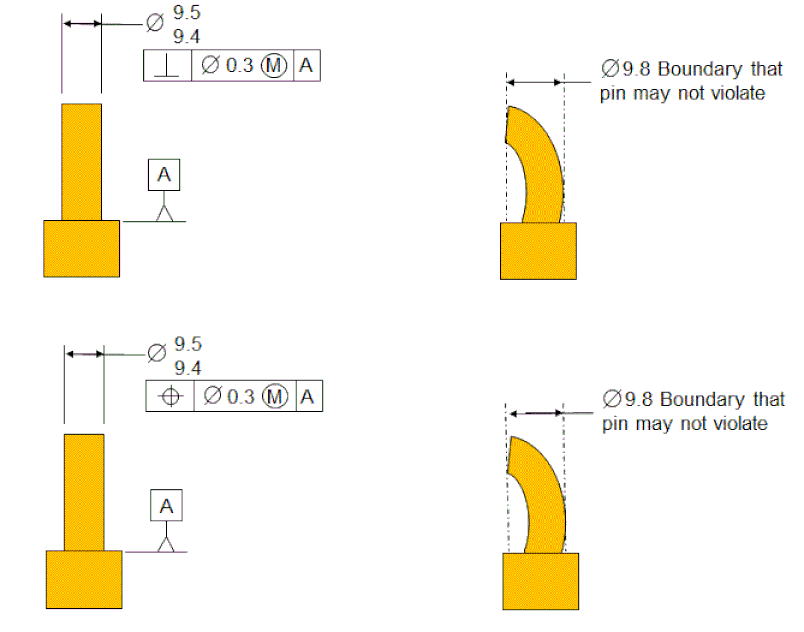
The figure below shows first a Perpendicularity and then a Tolerance Of Position. The top line shows the Perpendicularity callout and then the meaning of the Perpendicularity. In this case, since the Perpendicularity is called out MMC, it specifies a boundary that must not be violated. The boundary is perpendicular to datum [A], and the diameter of the boundary is equal to the Virtual Condition. In this case, the boundary is the MMC size of 9.5 plus the Perpendicularity of 0.3.
The bottom line shows the Tolerance Of Position callout on the left and the meaning on the right. The pin is restricted by exactly the same boundary as in the top line. Since the Tolerance Of Position is called out to datum [A] only, the boundary is not located relative to anything. Therefore the Tolerance Of Position has exactly the same meaning as the Perpendicularity.
The figure below shows first a Perpendicularity and then a Tolerance Of Position. The top line shows the Perpendicularity callout and then the meaning of the Perpendicularity. In this case, since the Perpendicularity is called out MMC, it specifies a boundary that must not be violated. The boundary is perpendicular to datum [A], and the diameter of the boundary is equal to the Virtual Condition. In this case, the boundary is the MMC size of 9.5 plus the Perpendicularity of 0.3.
The bottom line shows the Tolerance Of Position callout on the left and the meaning on the right. The pin is restricted by exactly the same boundary as in the top line. Since the Tolerance Of Position is called out to datum [A] only, the boundary is not located relative to anything. Therefore the Tolerance Of Position has exactly the same meaning as the Perpendicularity.
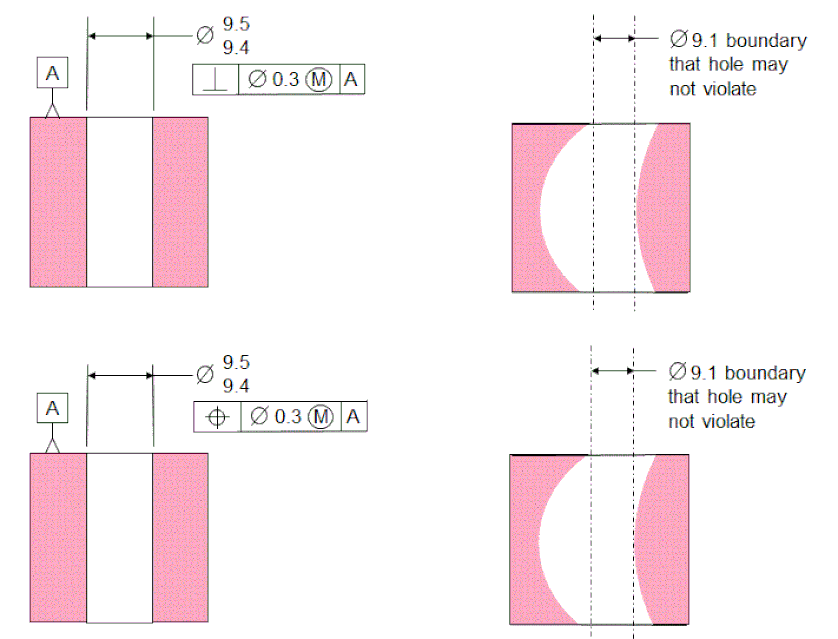
The next figure shows the same situation as above except with an internal Feature Of Size. The Perpendicularity specifies a 9.1 boundary inside the hole that must not be violated. The boundary is perpendicular to datum [A].
The Tolerance Of Position specifies exactly the same boundary. Again, this boundary is perpendicular to [A] but not located to any datums. So once again the Perpendicularity and the Tolerance of Position have exactly the same meaning.
The Tolerance Of Position specifies exactly the same boundary. Again, this boundary is perpendicular to [A] but not located to any datums. So once again the Perpendicularity and the Tolerance of Position have exactly the same meaning.
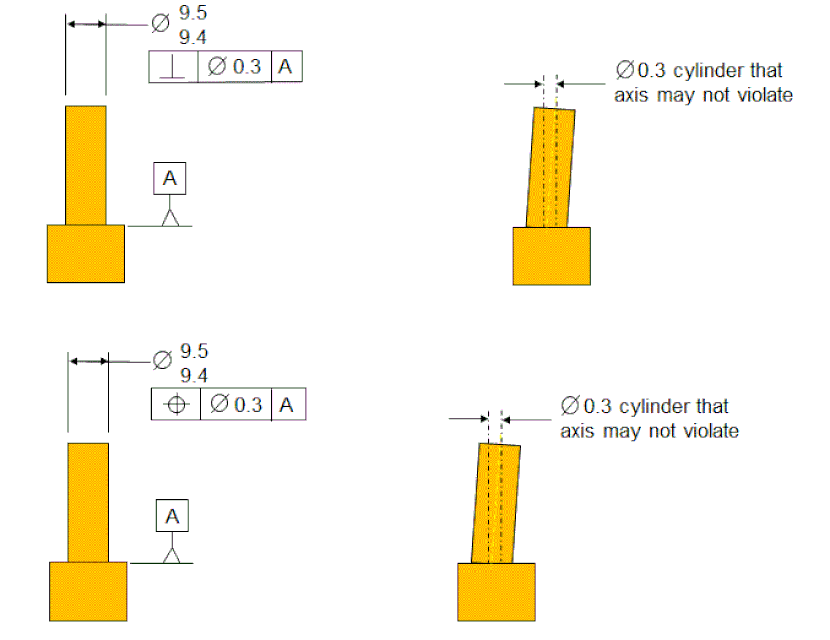
The next figure shows an external Feature Of Size with a Perpendicularity and a Tolerance Of Position both at RFS. In both cases, the axis of the pin must fall within a tolerance cylinder that is perpendicular to datum [A] and has diameter 0.3. In both cases, the tolerance cylinder is not located to any datums. Therefore the Perpendicularity and the Tolerance Of Position have exactly the same meaning.
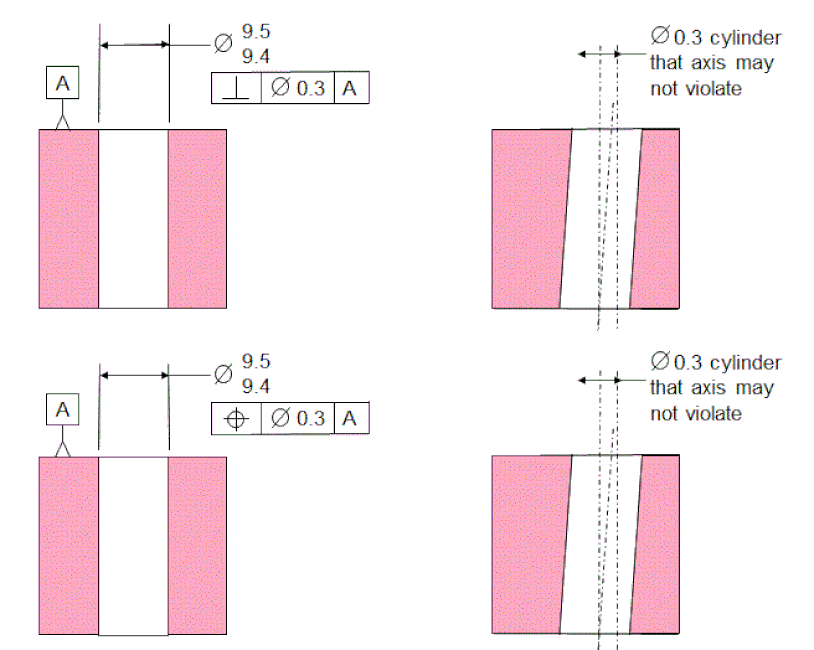
The final figure shows an internal Feature Of Size with Perpendicularity and Tolerance Of Position called out RFS. In both cases, the axis of the hole must fall within a tolerance cylinder that is perpendicular to datum [A] and has diameter 0.3. The tolerance cylinder is still not located to any datums, so the Tolerance Of Position and the Perpendicularity have exactly the same meaning.
Now let's review when to use RFS, MMC, and even LMC. This is a topic that causes much confusion.
I find that designers tend to want to either put MMC and MMB on all features of size or not use MMC and MMB at all. That's analogous to either putting commas after every word when writing or refusing to use any commas at all. Here is how that works in writing:
You might say: "Let's, eat, Grandma,"
but that makes no sense.
So you might say "Let's eat Grandma"
But now Grandma's life is in danger.
As a last resort, you might choose to put a comma where it makes sense and not where it does not make sense: "Let's eat, Grandma"
Now you and Grandma can finally enjoy a nice meal together.
In the same way, It makes a huge difference to the success of your company to put the MMC and MMB modifiers where they make sense for the good of the product and not where they would hurt the product. A drawing might have features of size with the MMC and MMB modifiers and others without them both in the same view.
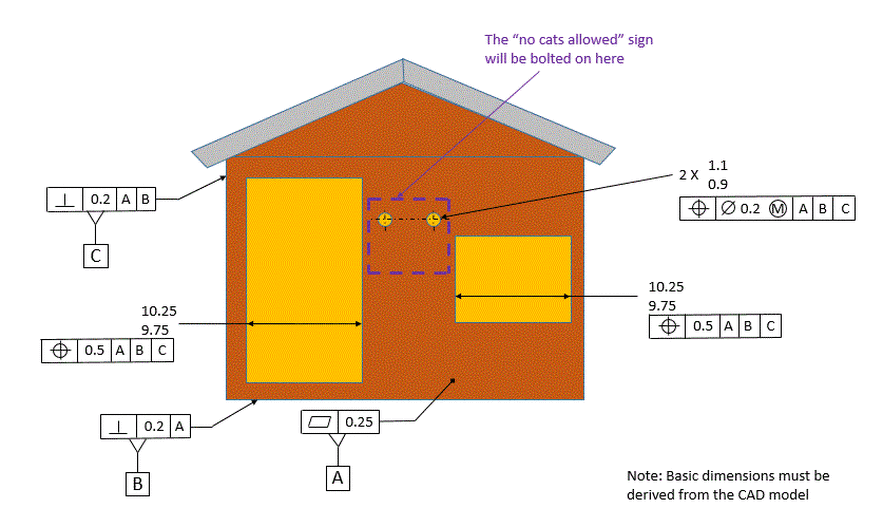
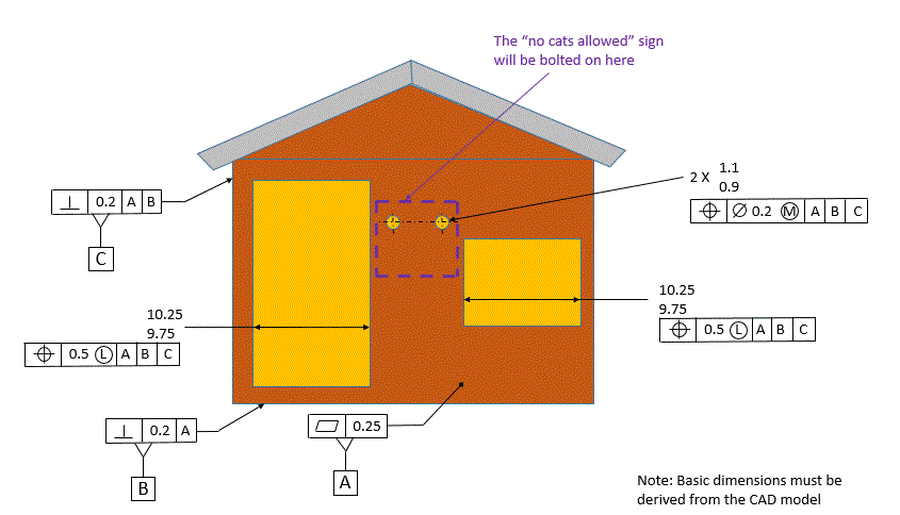
As an example, for the dog house below, the door and the window are both located by tolerance of position controls. The locations of the door and the window are fairly critical. We need to make sure that they do not get too near the outside walls. We also want to make sure we have enough room in between them to hang a "No Cats Allowed" sign that we will bolt to the clearance holes that are located between the door and the window.
If we were to use MMC on these features, that would allow extra location tolerance if the door or window is larger than its smallest allowable size. But we don't want extra location error just because the door or window is large. In fact, that could cause a problem. So we call them out RFS.
The location of the clearance holes for hanging the "No Cats Allowed" sign is not critical. We are going to have clearance holes in the sign also. Then we plan to just hold the sign up between the door and the window, line up the clearance holes so that the bolts go through, and put nuts on the other end of the bolts. So if the holes are larger than their smallest allowable size, it's okay to have the extra location tolerance permitted by the MMC callout. The bonus tolerance will make locating the holes easier and it will not hurt the function of the holes. So we want the MMC modifiers on the clearance holes for hanging the sign.
We can take it even one step farther. We mentioned that we want to preserve a minimum distance between the door and outer wall and between the window and outer wall. We also want to preserve a minimum distance between the door and the window. The most effective way to do this is with the LMC modifier on the tolerance of position for the door and the window. This will keep the location tolerance tight when either the door or the window is at it's largest size, and it will allow more location tolerance as the door or window get smaller than their largest allowable size. It provides the maximum amount of location tolerance possible while preserving the minimum distances we require between features.
In general, you should use:
RFS and RMB
RFS and RMB
- On critical features where bonus tolerance or datum feature shift cannot be tolerated
- Threaded holes
- Holes used in press fits
- Holes where you will use axi-rads
- Datums that are established by a gage ball. A gage ball has no size tolerance, so it makes no sense to reference it MMB.
- On non critical features where you are just concerned with assembly
- Threaded holes where fixed gaging is desired. However, if you do this, include a note stating that the tolerance applies to the MINOR DIA. Otherwise it will apply to the pitch diameter and defeat the whole purpose.
- Holes where you will use axi-rads but the supplier wants to use a fixed gage. Be careful here. The design might not tolerate the bonus or datum feature shift. Think it through before you agree to use MMC or MMB.
- Where you need to maintain a minimum wall thickness or other minimum distance
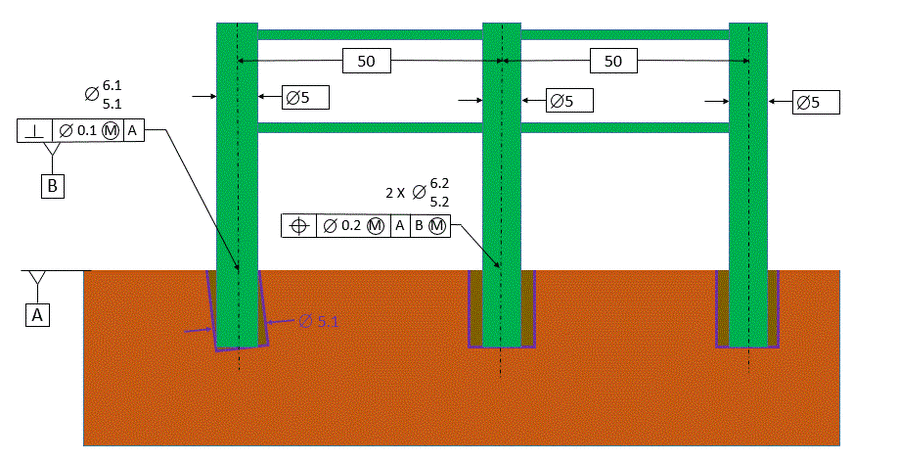
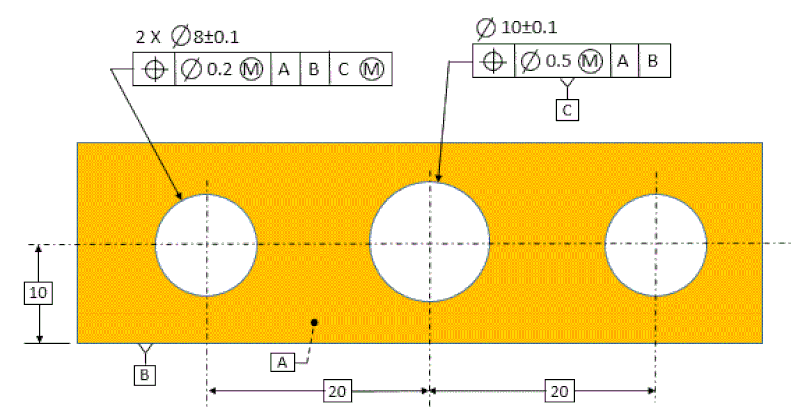
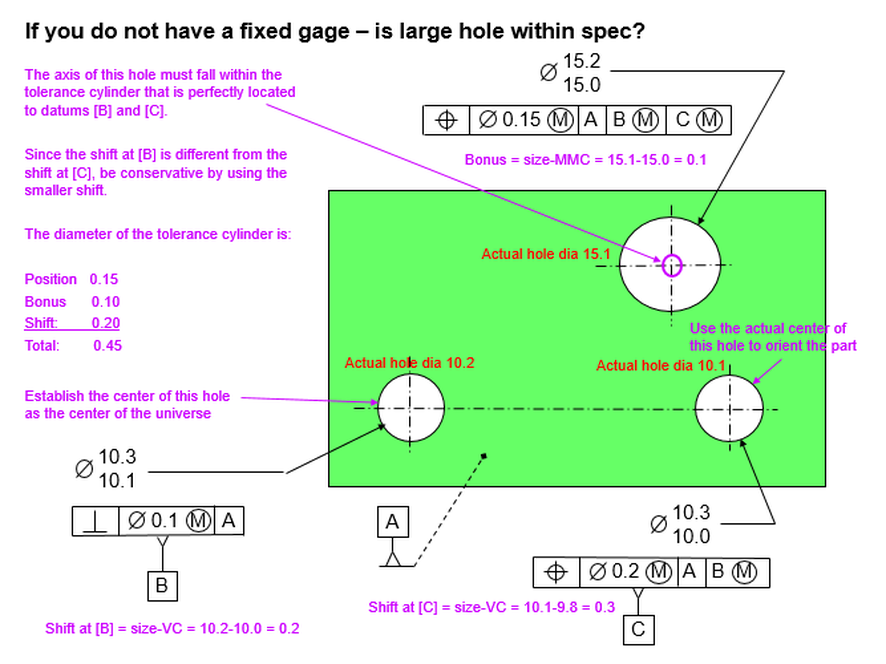
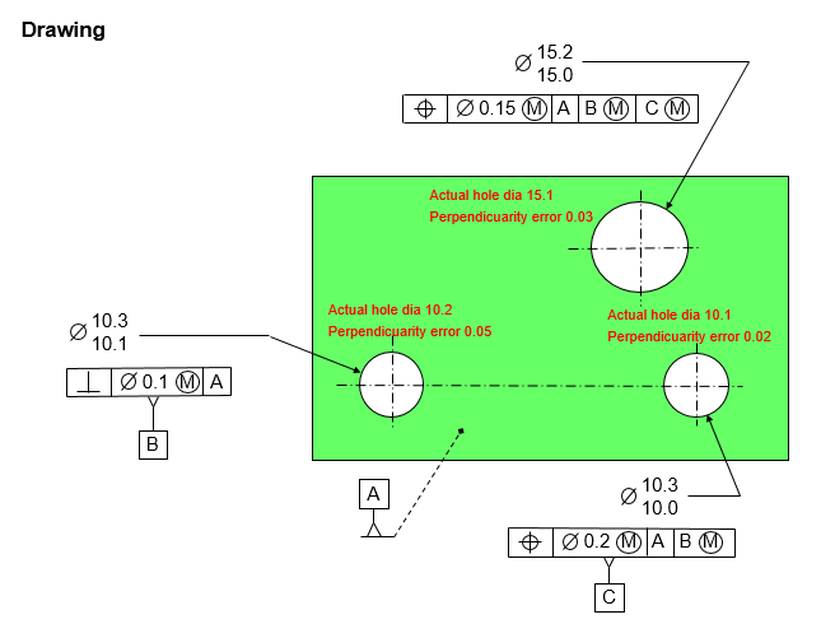
Now let's talk about datum feature shift relative to a pattern of holes.
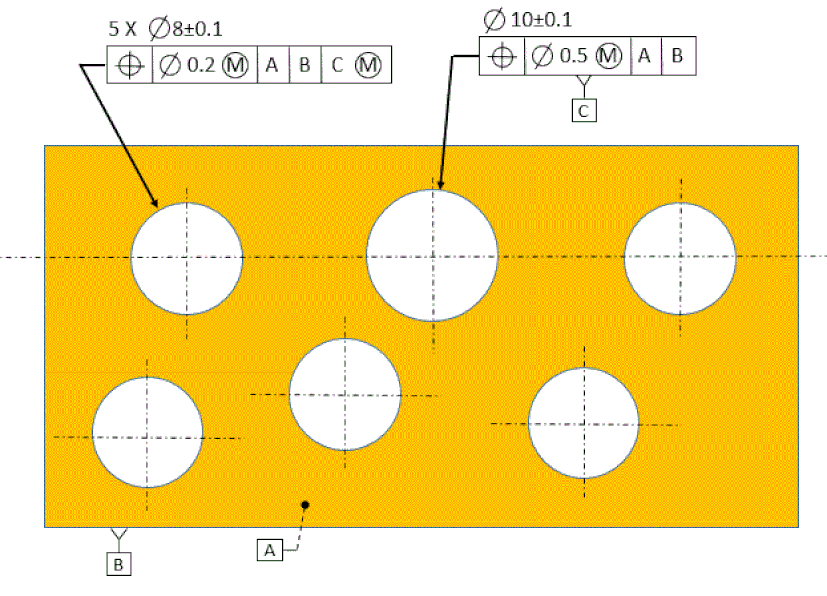
In the figure below, the outside holes are a pattern located relative to the center hole. Datum [C] is referenced MMB, so datum feature shift is allowed.
We see below how the part fits on a gage. The gage has a surface that represents datum [A] and another surface to represent datum [B]. There are three pins, each at the virtual condition size of their respective holes.
If the part has planar contact with [A] and line contact with [B] and at the same time slides over all of the pins, then it has met the tolerance of position requirements.
If the part has planar contact with [A] and line contact with [B] and at the same time slides over all of the pins, then it has met the tolerance of position requirements.
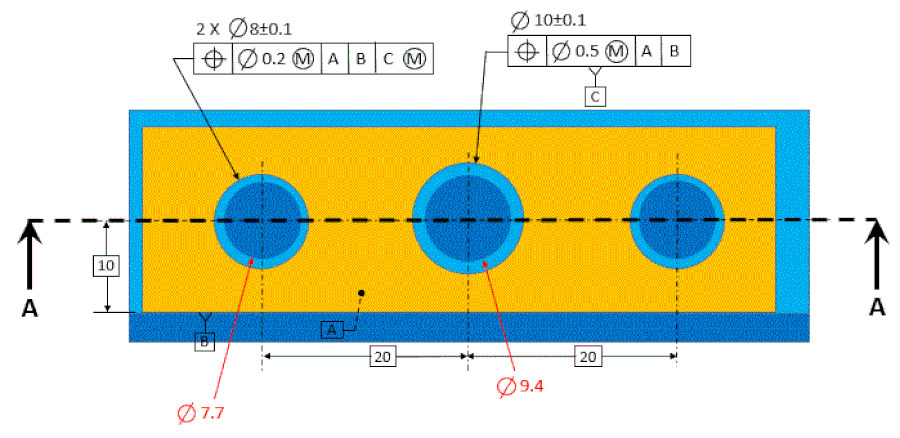
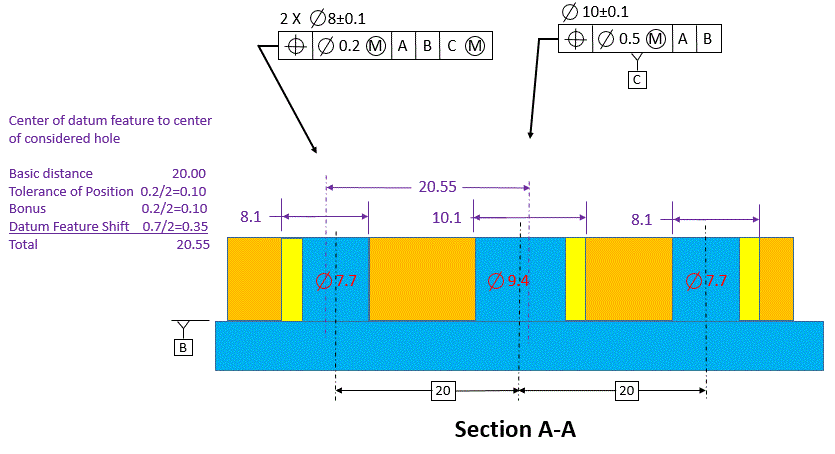
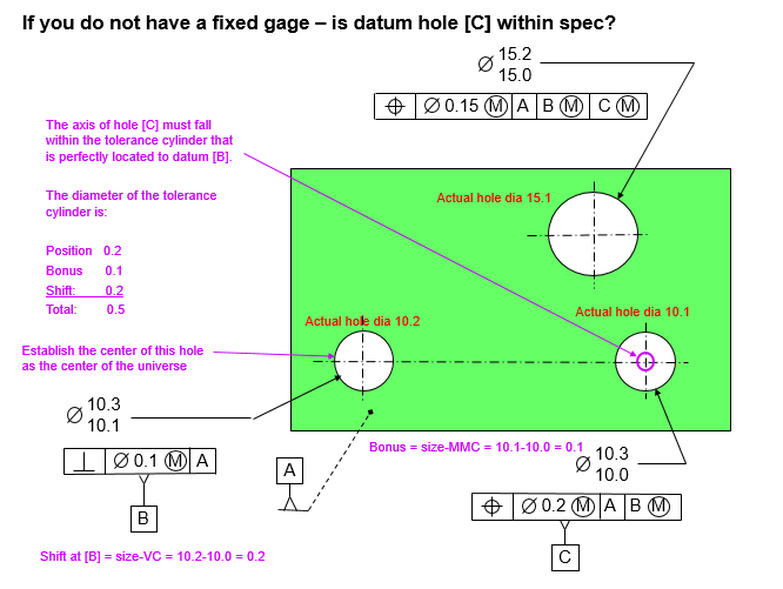
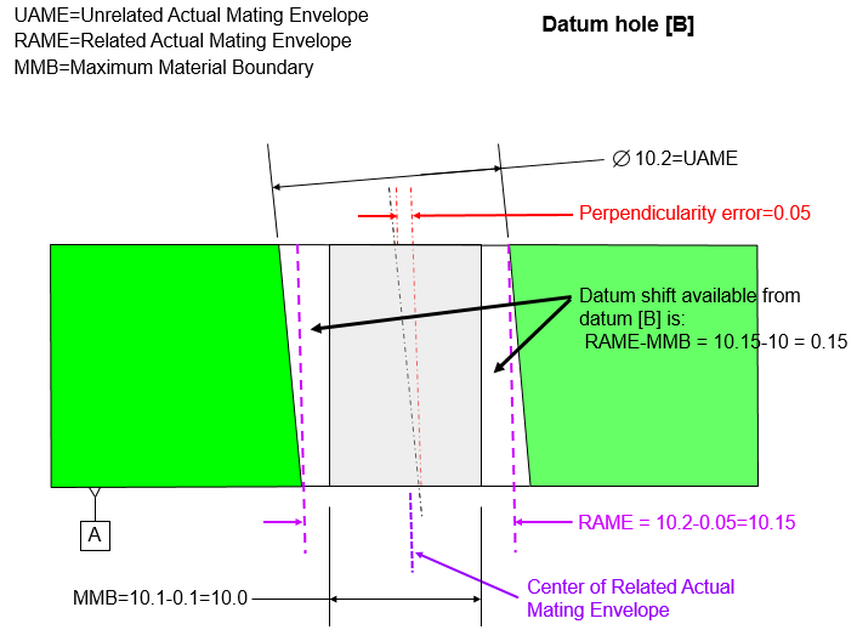
Now let's look at some extreme conditions. Cross section A-A shows how the holes interact with the pins. In this figure, the holes are at their LMC sizes and they are exactly perpendicular to datum [A]. This is the condition in which the holes can have their maximum allowable location error. Note that in the figure, the hole on the left is shifted as far as it can be to the left. The datum feature is shifted as far as it can shift to the right. So the center of the hole on the left is as far as it can legally be from the center of the datum feature.
To calculate the total distance that the hole on the left can be from the datum hole, take the basic 20 and add the radial position tolerance plus the radial bonus tolerance. Then add the radial datum feature shift. Remember that datum feature shift is the difference between the max hole and the gage. So it's 10.1-9.4=0.7. Divide by two for radial and we have 0.35.
Our total allowable center distance then between datum feature [C] and the center of the hole on the left is 20.55. If we were to measure the distance between these centers on a CMM and find them to be 20.55 or less, we would say that the hole on the left is within spec.
To calculate the total distance that the hole on the left can be from the datum hole, take the basic 20 and add the radial position tolerance plus the radial bonus tolerance. Then add the radial datum feature shift. Remember that datum feature shift is the difference between the max hole and the gage. So it's 10.1-9.4=0.7. Divide by two for radial and we have 0.35.
Our total allowable center distance then between datum feature [C] and the center of the hole on the left is 20.55. If we were to measure the distance between these centers on a CMM and find them to be 20.55 or less, we would say that the hole on the left is within spec.
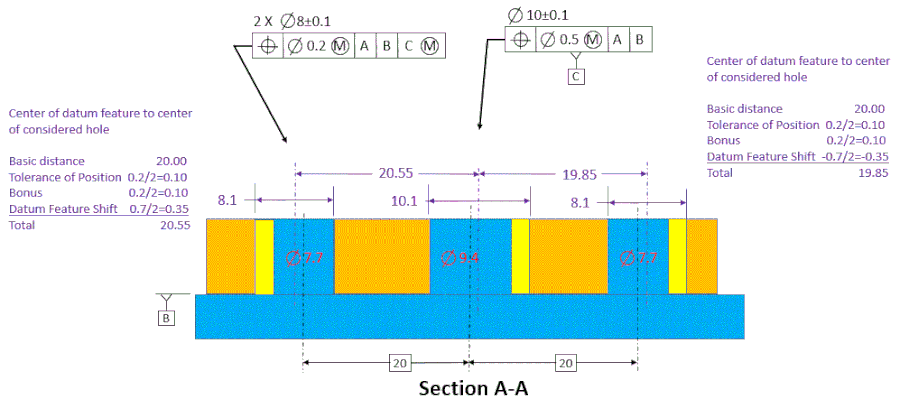
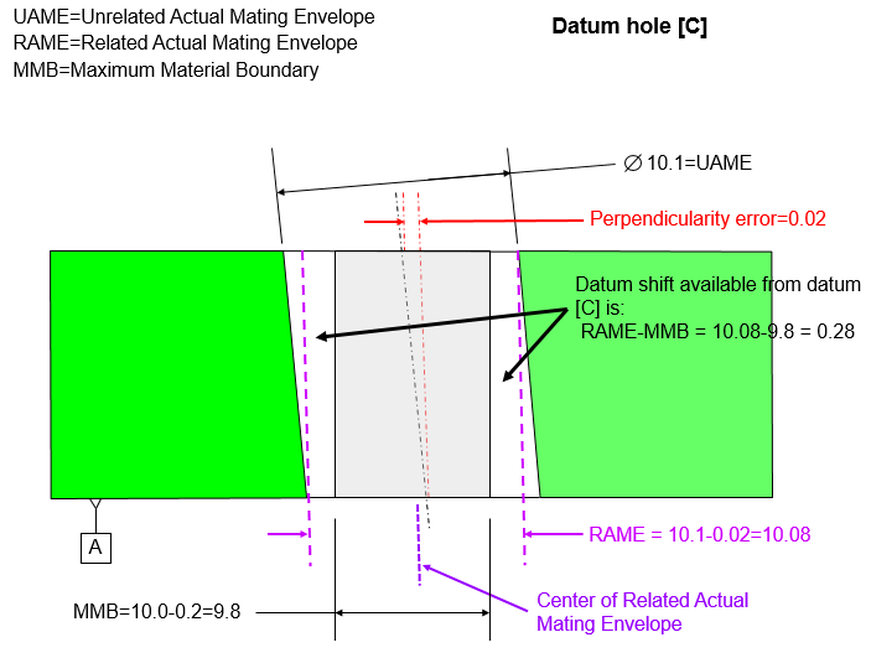
But what about the hole on the right? The datum feature is already shifted to the right. So in our calculations we must subtract the shift instead of adding it. The maximum we can have then between datum feature [C] and the hole on the right is 19.85.
What if we were to insist that the hole on the right should be able to add the shift just like the hole on the left? The part would not fit on the gage.
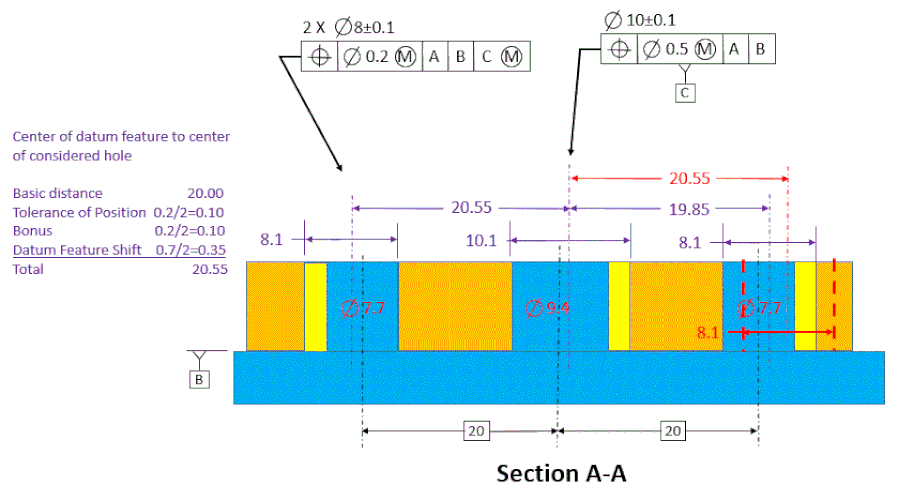
The caution here is that the datum feature can only shift in one direction relative to a pattern. If the shift increases the distance to one hole, it my decrease the distance to another hole. We need to keep this in mind when using a CMM to gage the holes. In this simple case, it's not too difficult to keep track of which is which.
The caution here is that the datum feature can only shift in one direction relative to a pattern. If the shift increases the distance to one hole, it my decrease the distance to another hole. We need to keep this in mind when using a CMM to gage the holes. In this simple case, it's not too difficult to keep track of which is which.
What if we have a more complex pattern with holes in odd locations? How are we going to keep track of which direction the datum feature might shift and therefore where to add the shift and where to subtract parts of it or all of it?
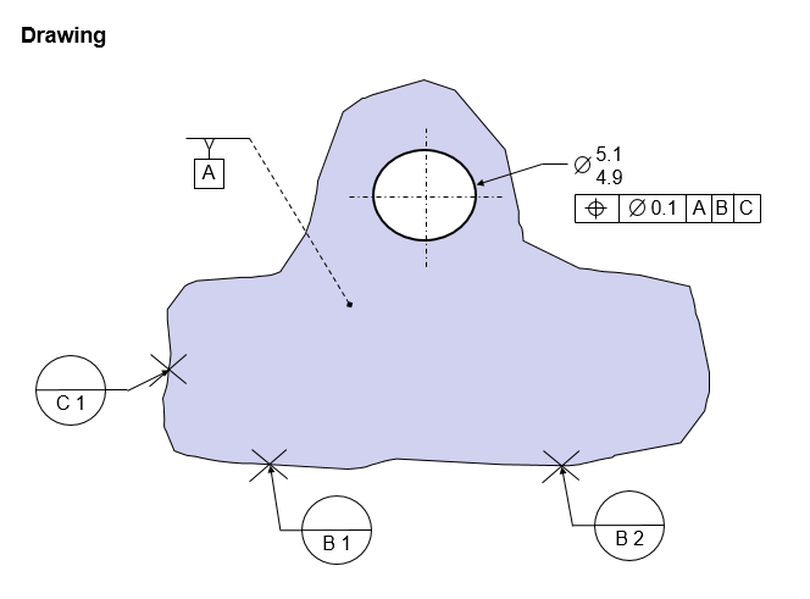
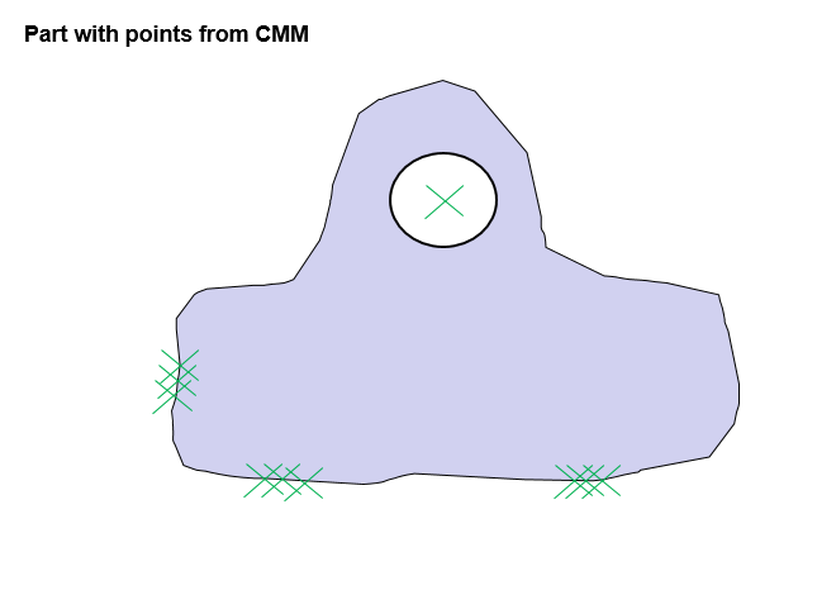
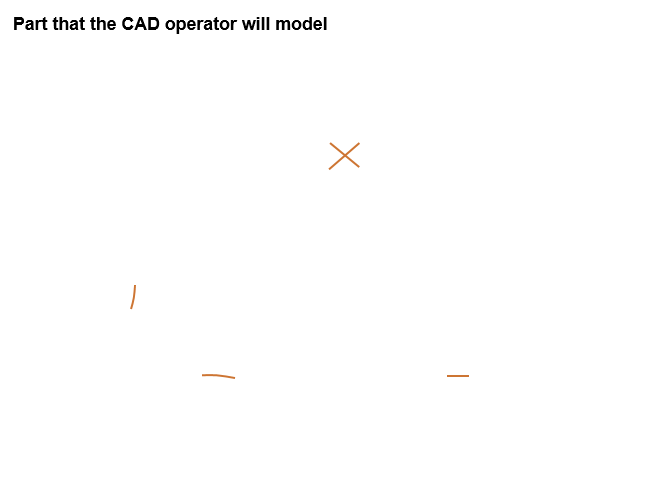
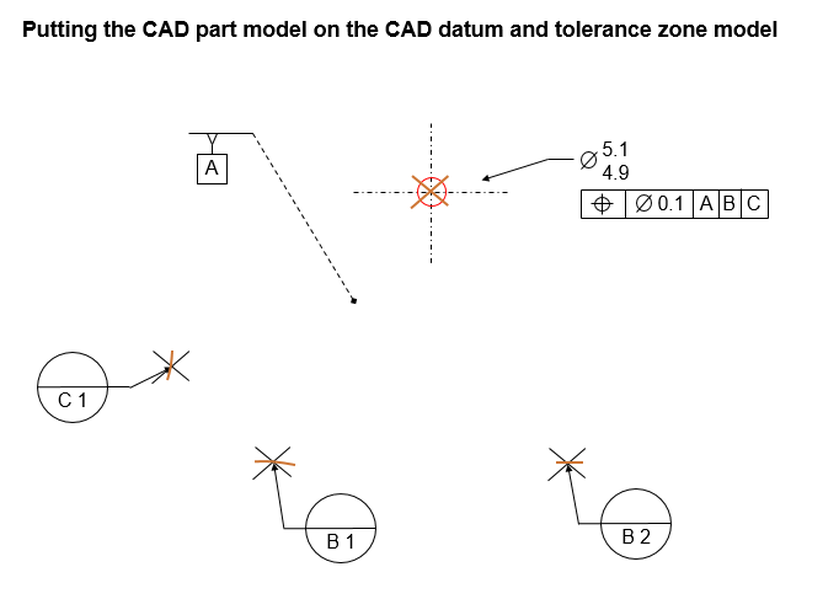
This is where I fall back on what I often tell a CMM operator. You are just going to need to use a fixed gage. Of course, you may not have that option. So then you need to befriend a CAD operator.
Probe your points like you normally would. You will probably take 3 points to establish plane [A], two points to establish [B], and three points at each of the holes.
Probe your points like you normally would. You will probably take 3 points to establish plane [A], two points to establish [B], and three points at each of the holes.
Give all of these coordinates to a CAD operator, and ask them to create a CAD model of your part as measured.
Ask them to also create a CAD model of the gage.
Then ask them in CAD to determine whether or not the part as measured fits on the gage. If the part fits, then it satisfies the tolerance of position requirements. If not, it's a bad part.
Let's take a look at the boundaries that are used when discussing Tolerance of Position.
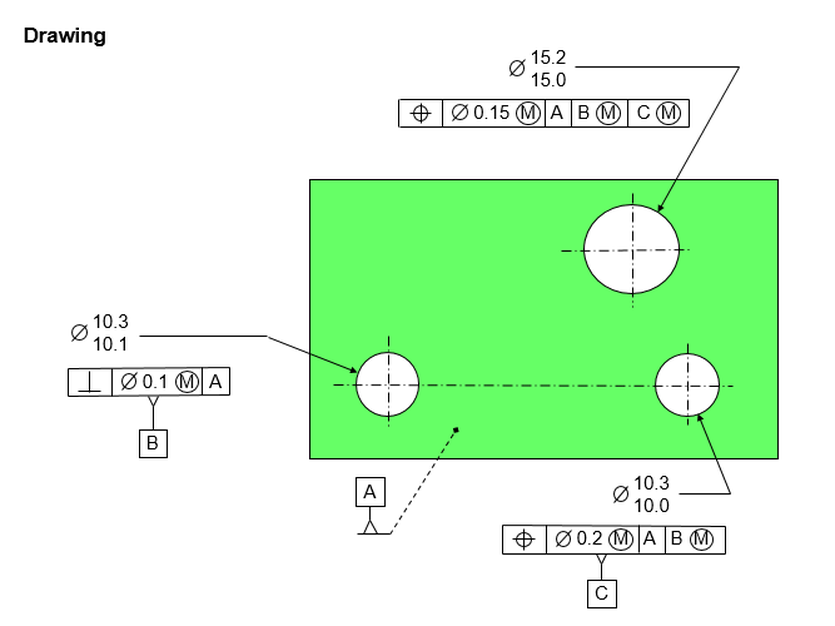
The figure below shows a datum feature hole on the left and a considered hole on the right.
Starting inside the considered hole, we have a MMC boundary. One could argue that MMC is not really a boundary, it's just a size. It's the smallest size that the hole is allowed to be. We also see the largest size that the hole is allowed to be, the LMC size.
Inside the considered hole we also see the Virtual Condition. The Virtual Condition really is a boundary. It's the boundary that will never be violated by the smallest allowable hole with the maximum position and/or perpendicularity error. The virtual condition boundary is exactly perpendicular to datum [A] and located perfectly by the basic dimension relative to datum [B].
Moving to the left, we see inside the datum feature hole the Max Material Boundary. It's really another virtual condition, but when it's applied to a datum feature of size all of the cool GD&T geeks call it a Max Material Boundary. The Max Material Boundary is the boundary that will not be violated by the smallest datum feature hole with the largest allowable perpendicularity error. The Max Material Boundary is perpendicular to datum [A].
We also see the Least Material Boundary. The Least Material Boundary is inside the material. The Least Material Boundary is the boundary that will not be violated by the largest allowable hole with the maximum allowable perpendicularity error. The Least Material Boundary is perpendicular to datum [A].
The figure below shows a datum feature hole on the left and a considered hole on the right.
Starting inside the considered hole, we have a MMC boundary. One could argue that MMC is not really a boundary, it's just a size. It's the smallest size that the hole is allowed to be. We also see the largest size that the hole is allowed to be, the LMC size.
Inside the considered hole we also see the Virtual Condition. The Virtual Condition really is a boundary. It's the boundary that will never be violated by the smallest allowable hole with the maximum position and/or perpendicularity error. The virtual condition boundary is exactly perpendicular to datum [A] and located perfectly by the basic dimension relative to datum [B].
Moving to the left, we see inside the datum feature hole the Max Material Boundary. It's really another virtual condition, but when it's applied to a datum feature of size all of the cool GD&T geeks call it a Max Material Boundary. The Max Material Boundary is the boundary that will not be violated by the smallest datum feature hole with the largest allowable perpendicularity error. The Max Material Boundary is perpendicular to datum [A].
We also see the Least Material Boundary. The Least Material Boundary is inside the material. The Least Material Boundary is the boundary that will not be violated by the largest allowable hole with the maximum allowable perpendicularity error. The Least Material Boundary is perpendicular to datum [A].
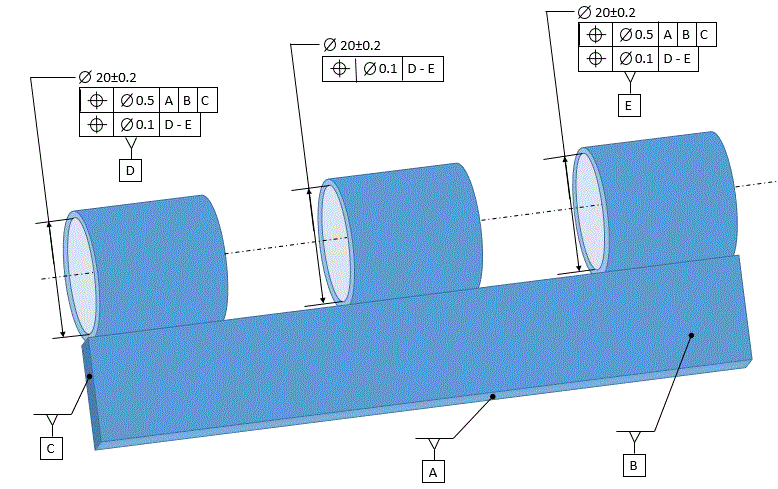
Sometimes we locate things relative to a datum that is derived from a combination of two datum features, each of which establishes a different datum. To further confuse things, we locate each of those datum features relative to the datum that is derived from them. So what does this mean?
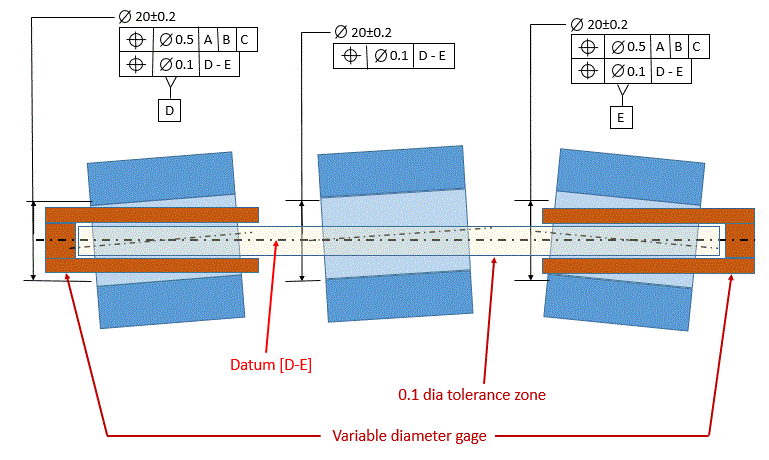
We have an example below. This is part of a hinge. A pin will go through the cylinders, so we want to have the cylinders lined up really well with each other. The holes on the ends are datums [D] and [E]. They are located to datums [A],[B], and [C] with a relatively large tolerance because the location relative to [A],[B], and [C] is not critical. All of the holes are located to [D-E] with a tight tolerance because the alignment of the holes to each other is critical.
We have an example below. This is part of a hinge. A pin will go through the cylinders, so we want to have the cylinders lined up really well with each other. The holes on the ends are datums [D] and [E]. They are located to datums [A],[B], and [C] with a relatively large tolerance because the location relative to [A],[B], and [C] is not critical. All of the holes are located to [D-E] with a tight tolerance because the alignment of the holes to each other is critical.
The figure below shows how all of this works. We will focus only on the position tolerances relative to the [D-E] datum.
Since datum [D-E] is referenced RMB, the gage that establishes datum [D-E] must be variable. The gage has two variable size pins that go into datum features [D] and [E]. These variable size pins are exactly in line with each other. They expand until they are snug in each of datum features [D] and [E].
Datum [D-E] is the axis from gage pin to gage pin.
The 0.1 diameter tolerance zone is exactly centered on datum [D-E].
The axis of each of the holes (the axis of the unrelated actual mating envelope of each of the holes) must fall within the 0.1 diameter tolerance zone.
For the center hole, it's easy to see how this aligns (locates and orients) it to the end holes.
So why do we need the location tolerance on the holes on the ends relative to the axis between the two holes? The holes on the ends are already automatically located to [D-E]. The location tolerance on [D] and [E] relative to [D-E] orients [D] and [E] relative to [D-E]. This is crucial in order to keep all three holes aligned so that the pin can go through.
Since datum [D-E] is referenced RMB, the gage that establishes datum [D-E] must be variable. The gage has two variable size pins that go into datum features [D] and [E]. These variable size pins are exactly in line with each other. They expand until they are snug in each of datum features [D] and [E].
Datum [D-E] is the axis from gage pin to gage pin.
The 0.1 diameter tolerance zone is exactly centered on datum [D-E].
The axis of each of the holes (the axis of the unrelated actual mating envelope of each of the holes) must fall within the 0.1 diameter tolerance zone.
For the center hole, it's easy to see how this aligns (locates and orients) it to the end holes.
So why do we need the location tolerance on the holes on the ends relative to the axis between the two holes? The holes on the ends are already automatically located to [D-E]. The location tolerance on [D] and [E] relative to [D-E] orients [D] and [E] relative to [D-E]. This is crucial in order to keep all three holes aligned so that the pin can go through.
The questions that I find the most difficult to answer come from operators of CMMs. They usually don't like the answers I give them. The discussion below will provide suggestions that may not be convenient, but they will be correct.
The discussion below will first address pattern datums and then address datum targets.
Consider the drawing below. Consider all dimensions to be basic. Only the holes are shown because the holes are the only part of the drawing that is important to this discussion.
Note that datum [B] consists of four holes. We normally like to describe the requirement by describing the gage or the fixture that would hold the part. In this case the gage would need to have four expanding pins at the basic locations of the datum holes, and each pin would need to expand as much as it can. How ever those four expanding pins end up holding the part is how the part needs to be held.
When I tell this to the CMM operator, he tells me that he does not have a fixture with four expanding pins located at the basic locations. He must determine a starting point and a direction in order to locate and orient the part.
Apparently the standard practice for the CMM operator, when faced with this situation, is to choose one of the four holes as an origin, choose the hole farthest away from the first point as the point that will establish a direction, and ignore the other two holes. It does not reflect the datum requirement, but it's the best he can do.
The discussion below will first address pattern datums and then address datum targets.
Consider the drawing below. Consider all dimensions to be basic. Only the holes are shown because the holes are the only part of the drawing that is important to this discussion.
Note that datum [B] consists of four holes. We normally like to describe the requirement by describing the gage or the fixture that would hold the part. In this case the gage would need to have four expanding pins at the basic locations of the datum holes, and each pin would need to expand as much as it can. How ever those four expanding pins end up holding the part is how the part needs to be held.
When I tell this to the CMM operator, he tells me that he does not have a fixture with four expanding pins located at the basic locations. He must determine a starting point and a direction in order to locate and orient the part.
Apparently the standard practice for the CMM operator, when faced with this situation, is to choose one of the four holes as an origin, choose the hole farthest away from the first point as the point that will establish a direction, and ignore the other two holes. It does not reflect the datum requirement, but it's the best he can do.
There is a way to gage this that does accurately reflect the datum requirement. It requires the CMM operator to develop a relationship with a CAD operator. I've never been a CMM operator, but I've been a CAD operator. I've had a CMM operator ask me to help him as shown below. It worked amazingly well.
The figure below shows basic locations These are the theoretically perfect locations referred to in the drawing. The bottom four are the perfect locations corresponding to datum [B], and the top one is the perfect location of what we will refer to as the considered hole (the hole that is being measured, the one that is not the datum).
The figure below shows basic locations These are the theoretically perfect locations referred to in the drawing. The bottom four are the perfect locations corresponding to datum [B], and the top one is the perfect location of what we will refer to as the considered hole (the hole that is being measured, the one that is not the datum).
The figure below shows the basic locations along with the corresponding tolerance zones.
The dimensioning requires first that the axis of the datum holes all be able to fit within their tolerance zones at the same time. If they don't, then it's already a bad part without even looking at the considered hole.
Once the axis of the datum holes are all within their respective tolerance zones, the axis of the considered hole also must fall within its tolerance zone at the same time that the axis of the datum holes are all within their tolerance zones.
At this point it is important to note that a CAD operator can model these perfect locations along with their tolerance zones.
The dimensioning requires first that the axis of the datum holes all be able to fit within their tolerance zones at the same time. If they don't, then it's already a bad part without even looking at the considered hole.
Once the axis of the datum holes are all within their respective tolerance zones, the axis of the considered hole also must fall within its tolerance zone at the same time that the axis of the datum holes are all within their tolerance zones.
At this point it is important to note that a CAD operator can model these perfect locations along with their tolerance zones.
The figure below shows the actual part. It is imperfect. It is what the CMM operator is required to measure. When the CMM operator looks at this real part, his first instinct is to establish an origin and a direction.
For purposes of this discussion, I suggest that the CMM operator establish locations of each of the datum holes and also the considered hole. Use any point for the origin. It does not matter. Direction also does not matter. As long as all five holes are measured at the same time, with a consistent coordinate system, it does not matter what that coordinate system is.
At this point it is important to note that a CAD operator can model this real, imperfect part based on the locations given to him by the CMM operator.
Now the CMM operator is done, and the rest is up to the CAD operator.
For purposes of this discussion, I suggest that the CMM operator establish locations of each of the datum holes and also the considered hole. Use any point for the origin. It does not matter. Direction also does not matter. As long as all five holes are measured at the same time, with a consistent coordinate system, it does not matter what that coordinate system is.
At this point it is important to note that a CAD operator can model this real, imperfect part based on the locations given to him by the CMM operator.
Now the CMM operator is done, and the rest is up to the CAD operator.
The CAD operator can take his model of the real, imperfect part and lay it over his model of the perfect locations with tolerance zones. He can move the actual part around relative to the tolerance zones.
First he must find a location and orientation in which the axis of the datum holes all fall within their tolerance zones at the same time. If he cannot do this, then it is a bad part.
Once the CAD operator has the actual part lined up with the datum tolerance zones, he must check to see whether or not the axis of the considered hole falls within its tolerance zone while the axis of the datum holes are within their tolerance zones. If it does, it's a good part. If not, then it's a bad part.
First he must find a location and orientation in which the axis of the datum holes all fall within their tolerance zones at the same time. If he cannot do this, then it is a bad part.
Once the CAD operator has the actual part lined up with the datum tolerance zones, he must check to see whether or not the axis of the considered hole falls within its tolerance zone while the axis of the datum holes are within their tolerance zones. If it does, it's a good part. If not, then it's a bad part.
Now let's add a little twist. Note that now the considered hole is called out MMC (Max Material Condition), and the datum is referenced MMB (Max Material Boundary). Now the considered hole must not violate its 4.7 dia Virtual Condition boundary at the same time that the datum holes are not violating their 10 dia Virtual Condition boundaries.
GD&T instructors love to tell you about the fixed gages that you can make, and if the part fits over the fixed gage, it's a good part.
If you are a CMM operator, you don't have fixed gages. Once again you are wondering how you can establish an origin and a direction. And how to you deal with bonus tolerance and datum feature shift?
I suggest, once again, that the CMM operator ask the CAD operator to create a model of the perfect locations with their Virtual Condition boundaries.
GD&T instructors love to tell you about the fixed gages that you can make, and if the part fits over the fixed gage, it's a good part.
If you are a CMM operator, you don't have fixed gages. Once again you are wondering how you can establish an origin and a direction. And how to you deal with bonus tolerance and datum feature shift?
I suggest, once again, that the CMM operator ask the CAD operator to create a model of the perfect locations with their Virtual Condition boundaries.
Once again the CMM operator can choose any coordinate system to establish locations and sizes of all holes on the actual part.
With this information, the CAD operator can model the actual part and then determine whether or not there is a condition in which the model of the actual part can fit over the model of the boundaries that the part must not violate.
The CAD operator has now electronically created a gage and a real part and determined whether or not the real part will fit over the gage.
With this information, the CAD operator can model the actual part and then determine whether or not there is a condition in which the model of the actual part can fit over the model of the boundaries that the part must not violate.
The CAD operator has now electronically created a gage and a real part and determined whether or not the real part will fit over the gage.
Now consider the part below with datum targets. Assume the part is dimensioned with basic dimensions. The explanation for this tolerancing scheme normally involves imagining a fixture with a flat surface for datum [A] and pins for targets B1,B2, and C1.
This is the actual part, which is what the CMM operator sees. He immediately starts thinking about how to establish an origin and a direction. He is at a loss as to how to do that.
Once again, if the CMM operator can establish a working relationship with a CAD operator, he can get some help.
Once again, if the CMM operator can establish a working relationship with a CAD operator, he can get some help.
If the CMM operator knows he can work with a CAD operator, then the CMM operator can choose any origin and angle. It doesn't matter. He should then probe points in the vicinity of where the datum targets are. He will not know exactly where on the part the datum targets will contact the part, so he should probe many points in the general area of each datum target. He should also probe the hole. Each green X below represents a point where the CMM operator probes. The CMM operator can then pass these points on to the CAD operator.
The CAD operator can connect points and create a model of the areas in the vicinity of the target points. This constitutes a model of the actual part.
The CAD operator can also create a model of the datum targets and the tolerance zone for the hole. This constitutes a model of the gage.
Now the CAD operator can fit the part model onto the gage model and determine whether or not the axis of the actual hole falls within the tolerance zone.
In both cases, with pattern datums and with datum targets, the explanation of the part requirement involved placing a part on a gage. The CMM operator was able to probe points, not based on any particular coordinate system, and give those points to a CAD operator. The CAD operator was able to electronically create the part and the gage, place the electronic part on the electronic gage, and determine whether or not the dimensional requirements were met.
Calculating Bonus and Shift
When I teach about the meaning of MMC and MMB, I show how to inspect the part with fixed gages. When the students who are CMM operators see pictures of fixed gages, they feel neglected because they cannot make fixed gages. They must probe parts and establish sizes and distances. This instruction shows how to approach parts with the MMC and MMB modifiers from the perspective of establishing hole centers and sizes and distances.
The principles below are mathematically sound, but they are also complicated. A much simpler solution, if available, would be to coordinate with a CAD operator. For a given part, you can gage your points and give the point coordinates to a CAD operator. The CAD operator can then create a CAD model of your part as measured, create a CAD model of the gage, and in CAD determine whether or not the part fits on the gage.
For those who do not have access to CAD, the explanation below describes the math you must do.
The explanation immediately below assumes that all holes are perfectly perpendicular to datum [A]. This will never happen, but it is a simplifying assumption that many people make. Further below is an explanation that includes perpendicularity error.
Consider the drawing below. The bottom holes are datum features called out MMC. The top hole is located relative to the datums, and those datums are referenced at MMB.
Consider these holes to be located relative to each other with basic dimensions.
Gaging this part involves three steps:
1. Determine whether or not hole [B] is in spec
2. Determine whether or not hole [C] is in spec
3. Determine whether or not the top hole is in spec
When I teach about the meaning of MMC and MMB, I show how to inspect the part with fixed gages. When the students who are CMM operators see pictures of fixed gages, they feel neglected because they cannot make fixed gages. They must probe parts and establish sizes and distances. This instruction shows how to approach parts with the MMC and MMB modifiers from the perspective of establishing hole centers and sizes and distances.
The principles below are mathematically sound, but they are also complicated. A much simpler solution, if available, would be to coordinate with a CAD operator. For a given part, you can gage your points and give the point coordinates to a CAD operator. The CAD operator can then create a CAD model of your part as measured, create a CAD model of the gage, and in CAD determine whether or not the part fits on the gage.
For those who do not have access to CAD, the explanation below describes the math you must do.
The explanation immediately below assumes that all holes are perfectly perpendicular to datum [A]. This will never happen, but it is a simplifying assumption that many people make. Further below is an explanation that includes perpendicularity error.
Consider the drawing below. The bottom holes are datum features called out MMC. The top hole is located relative to the datums, and those datums are referenced at MMB.
Consider these holes to be located relative to each other with basic dimensions.
Gaging this part involves three steps:
1. Determine whether or not hole [B] is in spec
2. Determine whether or not hole [C] is in spec
3. Determine whether or not the top hole is in spec
First we will see whether or not datum hole [B] is within spec.
The hole has two requirements. It has a size requirement and a perpendicularity requirement. Since we are assuming that all holes are exactly perpendicular to datum [A], you need only check the size. The center of hole [B] now becomes the center of the universe for our purposes.
Now we must determine whether or not datum hole [C] is within spec. Since at this point all we have is datum [A] and hole [B], there is not yet any accounting for rotation. So we can only determine whether or not hole [C] is the correct distance from hole [B].
Datum [B] is the center of hole [B]. At the exact specified basic distance from datum [B] is the tolerance cylinder for datum hole [C]. This tolerance cylinder is exactly perpendicular to datum [A]. The actual axis of hole [C] must fall within this tolerance cylinder.
The question is, what is the diameter of the tolerance cylinder at datum hole [C].
Datum hole [C] has an MMC modifier, so once again we must calculate bonus tolerance. The bonus tolerance is the actual hole size of 10.1 minus the MMC size of 10.0. So the bonus tolerance is 0.1.
Datum hole [C] also references datum [B] at MMB. So we must calculate datum feature shift. Datum feature shift is the actual hole size of 10.2 minus the VC hole size of 10.0 (VC = MMC-Geo Tol = 10.1-0.1). So the datum feature shift is 0.2.
The total diameter of the tolerance cylinder at datum hole [C] then is the position tolerance of 0.2 plus the bonus tolerance of 0.1 plus the datum feature shift of 0.2 for a total tolerance zone cylinder of 0.5.
Don't forget to also check to make sure the diameter of the hole meets the size requirement.
The hole has two requirements. It has a size requirement and a perpendicularity requirement. Since we are assuming that all holes are exactly perpendicular to datum [A], you need only check the size. The center of hole [B] now becomes the center of the universe for our purposes.
Now we must determine whether or not datum hole [C] is within spec. Since at this point all we have is datum [A] and hole [B], there is not yet any accounting for rotation. So we can only determine whether or not hole [C] is the correct distance from hole [B].
Datum [B] is the center of hole [B]. At the exact specified basic distance from datum [B] is the tolerance cylinder for datum hole [C]. This tolerance cylinder is exactly perpendicular to datum [A]. The actual axis of hole [C] must fall within this tolerance cylinder.
The question is, what is the diameter of the tolerance cylinder at datum hole [C].
Datum hole [C] has an MMC modifier, so once again we must calculate bonus tolerance. The bonus tolerance is the actual hole size of 10.1 minus the MMC size of 10.0. So the bonus tolerance is 0.1.
Datum hole [C] also references datum [B] at MMB. So we must calculate datum feature shift. Datum feature shift is the actual hole size of 10.2 minus the VC hole size of 10.0 (VC = MMC-Geo Tol = 10.1-0.1). So the datum feature shift is 0.2.
The total diameter of the tolerance cylinder at datum hole [C] then is the position tolerance of 0.2 plus the bonus tolerance of 0.1 plus the datum feature shift of 0.2 for a total tolerance zone cylinder of 0.5.
Don't forget to also check to make sure the diameter of the hole meets the size requirement.
Now we must determine whether or not the top hole is within spec. The requirement is that the axis of the hole must fall within a tolerance cylinder that is exactly perpendicular to datum [A] and exactly located to datums [B] and [C]. Remember that the center of the tolerance cylinder at hole [B] is defined as datum [B]. The center of the tolerance cylinder at hole [C] is defined as datum [C]. Once again the question is what is the diameter of the tolerance cylinder at the top hole.
The top hole has a Tolerance of Position with an MMC modifier, so we will have bonus tolerance. The value of the bonus tolerance is the actual hole size of 15.1 minus the MMC hole size of 15.0. So the bonus tolerance is 0.1.
The large hole also references datums [B] and [C] at MMB, so we must consider datum feature shift. We already calculated the datum feature shift at hole [B]. The datum feature shift at hole [C] is the actual hole size of 10.1 minus the virtual condition of 9.8 (MMC - geo tol = 10.0-0.2 = 9.8). So the datum feature shift at hole [C] is 10.1-9.8=0.3.
For our tolerance cylinder at the large hole, we have a little bit of a dilemma. The datum feature shift relative to datum [C] is not the same size as that relative to datum [B]. Technically that makes our tolerance zone oblong rather than round. But we cannot mathematically deal with an oblong tolerance zone. So we will just be conservative and choose the smaller datum feature shift value which is the hole [B] value of 0.2.
So our total tolerance zone diameter at hole [C] is the tolerance of position value of 0.15 plus the bonus tolerance of 0.1 plus the datum feature shift of 0.2 for a total tolerance zone diameter of 0.45.
Once again remember to also check to make sure the diameter of the hole meets the size requirement.
The top hole has a Tolerance of Position with an MMC modifier, so we will have bonus tolerance. The value of the bonus tolerance is the actual hole size of 15.1 minus the MMC hole size of 15.0. So the bonus tolerance is 0.1.
The large hole also references datums [B] and [C] at MMB, so we must consider datum feature shift. We already calculated the datum feature shift at hole [B]. The datum feature shift at hole [C] is the actual hole size of 10.1 minus the virtual condition of 9.8 (MMC - geo tol = 10.0-0.2 = 9.8). So the datum feature shift at hole [C] is 10.1-9.8=0.3.
For our tolerance cylinder at the large hole, we have a little bit of a dilemma. The datum feature shift relative to datum [C] is not the same size as that relative to datum [B]. Technically that makes our tolerance zone oblong rather than round. But we cannot mathematically deal with an oblong tolerance zone. So we will just be conservative and choose the smaller datum feature shift value which is the hole [B] value of 0.2.
So our total tolerance zone diameter at hole [C] is the tolerance of position value of 0.15 plus the bonus tolerance of 0.1 plus the datum feature shift of 0.2 for a total tolerance zone diameter of 0.45.
Once again remember to also check to make sure the diameter of the hole meets the size requirement.
Below this point is an explanation that includes orientation error.
Now we will consider the entire design including orientation. Below is the drawing along with information about actual sizes and orientations of the holes.
In order to understand how to address orientation, it is necessary to take a close look at each of the holes.
Datum hole [B] is shown in the figure below. It's important to become familiar with certain terms which are listed in the upper left corner of the figure:
The UAME is the largest perfect cylinder that will fit inside the hole regardless of the orientation.
The RAME is the largest perfect cylinder that is exactly perfectly perpendicular to datum [A] and still fits within the hole.
The MMB is the smallest boundary that the hole will never be allowed to violate. It is the boundary that represents what the gage pin would be if we had a fixed pin gage.
Datum feature shift that will be available if the datum is referenced MMB is the space between the RAME and the MMB.
Also note the location of the center of the RAME.
Datum hole [B] is shown in the figure below. It's important to become familiar with certain terms which are listed in the upper left corner of the figure:
The UAME is the largest perfect cylinder that will fit inside the hole regardless of the orientation.
The RAME is the largest perfect cylinder that is exactly perfectly perpendicular to datum [A] and still fits within the hole.
The MMB is the smallest boundary that the hole will never be allowed to violate. It is the boundary that represents what the gage pin would be if we had a fixed pin gage.
Datum feature shift that will be available if the datum is referenced MMB is the space between the RAME and the MMB.
Also note the location of the center of the RAME.
Datum hole [C] is similar to datum hole [B]. Only the sizes are different.
The top hole has the same boundaries as the datum holes but with some slightly different terminology. The boundary that the hole is not allowed to violate is now the VC instead of the MMB. The space between the RAME and the VC is not called datum feature shift. Now this space is just calculated as RAME-VC.
For gaging the holes, we will look separately at orientation and location. First we will look at orientation.
For orientation, each hole’s axis (the axis of the UAME) must fall within a tolerance cylinder equal to its geometric tolerance plus its bonus tolerance.
For hole [B], the axis of the UAME must be oriented within a tolerance cylinder equal to the perpendicularity of 0.1 plus the bonus of 0.1 for a total of 0.2.
For hole [C], the axis of the UAME must be oriented within a tolerance cylinder equal to the Tolerance of Position of 0.2 plus the bonus of 0.1 for a total of 0.3.
For the top hole, the axis of the UAME must be oriented within a tolerance cylinder equal to the Tolerance of Position of 0.15 plus the bonus of 0.1 for a total of 0.25.
For orientation, each hole’s axis (the axis of the UAME) must fall within a tolerance cylinder equal to its geometric tolerance plus its bonus tolerance.
For hole [B], the axis of the UAME must be oriented within a tolerance cylinder equal to the perpendicularity of 0.1 plus the bonus of 0.1 for a total of 0.2.
For hole [C], the axis of the UAME must be oriented within a tolerance cylinder equal to the Tolerance of Position of 0.2 plus the bonus of 0.1 for a total of 0.3.
For the top hole, the axis of the UAME must be oriented within a tolerance cylinder equal to the Tolerance of Position of 0.15 plus the bonus of 0.1 for a total of 0.25.
With the orientation defined, we can look at location. Location now means location of the center of the RAME.
For location, consider what would happen if we were using a fixed gage. The location of the hole would be controlled by the looseness of the datum hole on the gage (datum feature shift) and the looseness of the considered hole on the gage. The looseness of the considered hole on the gage would be the diameter of the RAME minus the VC.
Note that there are no location issues with hole [B]. Hole [B] is the center of the universe.
For hole [C]:
When locating on the RAME of hole [B], the RAME of hole [C] must fall within a tolerance cylinder as described below:
RAME-VC = 10.08-9.8 = 0.28
Datum feature shift from datum [B] = 0.15
Total diameter of the tolerance cylinder for locating the center of the RAME of hole [C] is 0.28+0.15 = 0.43
For the upper hole:
Remember that when locating the upper hole, the part must be located by the center of the RAME of hole [B] and oriented by the center of the RAME of hole [C]. The calculations for the location tolerance cylinder for the RAME of the upper hole are:
RAME-VC = 15.07-14.85 = 0.22
Datum feature shift from datum [B] = 0.15
Datum feature shift from datum [C] = 0.28
To be conservative, we will use the smaller datum feature shift value.
Total diameter of the tolerance cylinder for locating the center of the RAME of the upper hole is 0.22+0.15 = 0.37
For location, consider what would happen if we were using a fixed gage. The location of the hole would be controlled by the looseness of the datum hole on the gage (datum feature shift) and the looseness of the considered hole on the gage. The looseness of the considered hole on the gage would be the diameter of the RAME minus the VC.
Note that there are no location issues with hole [B]. Hole [B] is the center of the universe.
For hole [C]:
When locating on the RAME of hole [B], the RAME of hole [C] must fall within a tolerance cylinder as described below:
RAME-VC = 10.08-9.8 = 0.28
Datum feature shift from datum [B] = 0.15
Total diameter of the tolerance cylinder for locating the center of the RAME of hole [C] is 0.28+0.15 = 0.43
For the upper hole:
Remember that when locating the upper hole, the part must be located by the center of the RAME of hole [B] and oriented by the center of the RAME of hole [C]. The calculations for the location tolerance cylinder for the RAME of the upper hole are:
RAME-VC = 15.07-14.85 = 0.22
Datum feature shift from datum [B] = 0.15
Datum feature shift from datum [C] = 0.28
To be conservative, we will use the smaller datum feature shift value.
Total diameter of the tolerance cylinder for locating the center of the RAME of the upper hole is 0.22+0.15 = 0.37